题目内容
过抛物线x2=4y上不同两点A、B分别作抛物线的切线相交于P点,
•
=0.
(1)求点P的轨迹方程;
(2)已知点F(0,1),是否存在实数λ使得
•
+λ(
)2=0?若存在,求出λ的值,若不存在,请说明理由.
| PA |
| PB |
(1)求点P的轨迹方程;
(2)已知点F(0,1),是否存在实数λ使得
| FA |
| FB |
| FP |
解法(一):(1)设A(x1,
),
由x2=4y,得:y′=
,∴kPA=
,kPB=
∵
•
=0,
∴PA⊥PB,∴x1x2=-4.(4分)
直线PA的方程是:y-
=
(x-x1)即y=
-
①
同理,直线PB的方程是:y=
-
②,(6分)
由①②得:
(x1,x2∈R)
∴点P的轨迹方程是y=-1(x∈R).(8分)
(2)由(1)得:
=(x1,
-1),
=(x2,
-1),P(
,-1)
=(
,-2),x1x2=-4,
•
=x1x2+(
-1)(
-1)=-2-
(
)2+2,
所以
•
+(
)2=0
故存在λ=1使得
•
+λ(
)2=0.(14分)
解法(二):(1)∵直线PA、PB与抛物线相切,且
•
=0,
∴直线PA、PB的斜率均存在且不为0,且PA⊥PB,
设PA的直线方程是y=kx+m(k,m∈R,k≠0)
由
得:x2-4kx-4m=0.(4分)
∴△=16k2+16m=0即m=-k2
即直线PA的方程是:y=kx-k2
同理可得直线PB的方程是:y=-
x-
,(6分)
由
得:
故点P的轨迹方程是y=-1(x∈R).(8分)
(2)由(1)得:A(2k,k2),B(-
,
-1),
∴
=(2k,k2-1),
=(-
,
-1),
=(k-
,-2)
•
=-4+(k2-1)(
-1)=-2-(k2+
).
故存在λ=1使得
•
+λ(
)2=0.(14分)
| x12 |
| 4 |
由x2=4y,得:y′=
| x |
| 2 |
| x1 |
| 2 |
| x2 |
| 2 |
| PA |
| PB |
∴PA⊥PB,∴x1x2=-4.(4分)
直线PA的方程是:y-
| ||
| 4 |
| x1 |
| 2 |
| x1x |
| 2 |
| ||
| 4 |
同理,直线PB的方程是:y=
| x2x |
| 2 |
| ||
| 4 |
由①②得:
|
∴点P的轨迹方程是y=-1(x∈R).(8分)
(2)由(1)得:
| FA |
| ||
| 4 |
| FB |
| ||
| 4 |
| x1+x2 |
| 2 |
| FP |
| x1+x2 |
| 2 |
| FA |
| FB |
| ||
| 4 |
| ||
| 4 |
| ||||
| 4 |
| FP |
所以
| FA |
| FB |
| FP |
故存在λ=1使得
| FA |
| FB |
| FP |
解法(二):(1)∵直线PA、PB与抛物线相切,且
| PA |
| PB |
∴直线PA、PB的斜率均存在且不为0,且PA⊥PB,
设PA的直线方程是y=kx+m(k,m∈R,k≠0)
由
|
∴△=16k2+16m=0即m=-k2
即直线PA的方程是:y=kx-k2
同理可得直线PB的方程是:y=-
| 1 |
| k |
| 1 |
| k2 |
由
|
|
故点P的轨迹方程是y=-1(x∈R).(8分)
(2)由(1)得:A(2k,k2),B(-
| 2 |
| k |
| 1 |
| k2 |
∴
| FA |
| FB |
| 2 |
| k |
| 1 |
| k2 |
| FP |
| 1 |
| k |
| FA |
| FB |
| 1 |
| k2 |
| 1 |
| k2 |
故存在λ=1使得
| FA |
| FB |
| FP |

练习册系列答案
相关题目
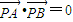 .
.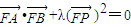 ?若存在,求出λ的值,若不存在,请说明理由.
?若存在,求出λ的值,若不存在,请说明理由.