题目内容
(2012•道里区二模)过抛物线x2=4y上不同两点A、B分别作抛物线的切线相交于点P(x0,y0),
•
=0.
(1)求y0;
(2)求证:直线AB恒过定点;
(3)设(2)中直线AB恒过定点F,是否存在实数λ,使
•
+λ(
)2=0恒成立?若存在,求出λ的值,若不存在,请说明理由.
| PA |
| PB |
(1)求y0;
(2)求证:直线AB恒过定点;
(3)设(2)中直线AB恒过定点F,是否存在实数λ,使
| FA |
| FB |
| FP |
分析:(1)设A,B的坐标,求得直线PA、PB的方程,利用
•
=0,可得y0;
(2)求出直线AB的方程,令x=0,结合(1)的结论,即可证得直线AB恒过定点;
(3)利用坐标表示向量,结合数量积公式,即可得到结论.
| PA |
| PB |
(2)求出直线AB的方程,令x=0,结合(1)的结论,即可证得直线AB恒过定点;
(3)利用坐标表示向量,结合数量积公式,即可得到结论.
解答:(1)解:设A(x1,
),B(x2,
),(x1≠x2).
由x2=4y,得:y′=
,∴kPA=
,kPB=
∵
•
=0,∴PA⊥PB,∴x1x2=-4.
直线PA的方程是:y-
=
(x-x1),即y=
-
.①
同理,直线PB的方程是:y=
-
.②
由①②得:y0=
=-1,(x1,x2∈R).…(4分)
(2)证明:由(1)可得直线AB的方程为y-
=
(x-x1)
令x=0,可得y-
=
•(-x1),
∵
=-1,∴y=1
∴直线AB恒过点(0,1)…(8分)
(3)解:由(1)得:
=(x1,
-1),
=(x2,
-1),x1x2=-4,
∴
•
=x1x2+(
-1)(
-1)=-2-
∵P=(
,-1),∴
=(
,-2),
∴(
)2=
+4=
+2,
∴
•
+(
)2=0.
故存在λ=1使得
•
+λ(
)2=0.…(12分)
| ||
| 4 |
| ||
| 4 |
由x2=4y,得:y′=
| x |
| 2 |
| x1 |
| 2 |
| x2 |
| 2 |
∵
| PA |
| PB |
直线PA的方程是:y-
| ||
| 4 |
| x1 |
| 2 |
| x1x |
| 2 |
| ||
| 4 |
同理,直线PB的方程是:y=
| x2x |
| 2 |
| ||
| 4 |
由①②得:y0=
| x1x2 |
| 4 |
(2)证明:由(1)可得直线AB的方程为y-
| ||
| 4 |
| ||||||||
| x2-x1 |
令x=0,可得y-
| ||
| 4 |
| x2+x1 |
| 4 |
∵
| x1x2 |
| 4 |
∴直线AB恒过点(0,1)…(8分)
(3)解:由(1)得:
| FA |
| ||
| 4 |
| FB |
| ||
| 4 |
∴
| FA |
| FB |
| ||
| 4 |
| ||
| 4 |
| ||||
| 4 |
∵P=(
| x1+x2 |
| 2 |
| FP |
| x1+x2 |
| 2 |
∴(
| FP |
| (x1+x2)2 |
| 4 |
| ||||
| 4 |
∴
| FA |
| FB |
| FP |
故存在λ=1使得
| FA |
| FB |
| FP |
点评:本题考查直线与抛物线的位置关系,考查直线恒过定点,考查向量知识的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
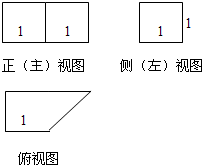 (2012•道里区二模)一个几何体的三视图如图所示,则该几何体的体积为( )
(2012•道里区二模)一个几何体的三视图如图所示,则该几何体的体积为( )