题目内容
设函数f(x)=g(x)+x2,曲线y=g(x)在点(1,g(1))处的切线方程为y=2x+1,则曲线y=f(x)在点(1,f(1))处的切线的斜率为( )
| A.2 | B.- | C.4 | D.- |
C
因为曲线y=g(x)在点(1,g (1))处的切线方程为y=2x+1,所以g'(1)=2.又f'(x)=g'(x)+2x,故曲线y=f(x)在点(1,f(1))处的切线的斜率为f'(1)=g'(1)+2=4.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
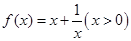 ,以点
,以点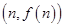 为切点作函数图像的切线
为切点作函数图像的切线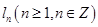 ,直线
,直线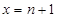 与函数
与函数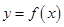 图像及切线
图像及切线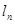 分别相交于
分别相交于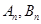 ,记
,记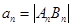 .
.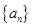 的通项;
的通项;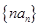 的前
的前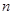 项和为
项和为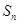 ,求证:
,求证: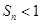 .
. ;
;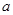 >0,试判断f(x)在定义域内的单调性;
>0,试判断f(x)在定义域内的单调性;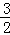 ,求
,求 上恒成立,求a的取值范围.
上恒成立,求a的取值范围.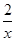 -3ln x,其中a为常数.
-3ln x,其中a为常数.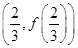 处的切线的斜率为1时,求函数f(x)在
处的切线的斜率为1时,求函数f(x)在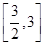 上的最小值;
上的最小值; x3+
x3+ ,
,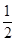 x2(a>0),若对定义域内的任意x,f′(x)≥2恒成立,则a的取值范围是________.
x2(a>0),若对定义域内的任意x,f′(x)≥2恒成立,则a的取值范围是________.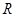 上的可导函数
上的可导函数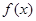 ,恒有
,恒有 ,(其中
,(其中 表示函数
表示函数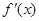 在
在 的值),则
的值),则