题目内容
设a为实数,函数f(x)=ex-2x+2a,x∈R.
(1)求f(x)的单调区间及极值;
(2)求证:当a>ln2-1且x >0时,ex>x2-2ax+1
(1)求f(x)的单调区间及极值;
(2)求证:当a>ln2-1且x >0时,ex>x2-2ax+1
(1)  (2)见解析
(2)见解析
 (2)见解析
(2)见解析试题分析:(1)首先求出
 的导数
的导数 ,解方程
,解方程 ,进一步得到不等式
,进一步得到不等式 与
与 的解集,从而得到函数的单调区间和极值.
的解集,从而得到函数的单调区间和极值.(2)欲证当a>ln2-1且x >0时,ex>x2-2ax+1,
令

则只需证当
 时,
时,
从而转化为利用导数求
 的最小值问题.
的最小值问题.试题解析:解:(1)由
 知
知
令
 得
得 于是当
于是当 变化时,
变化时, 的变化情况如下表:
的变化情况如下表: |  |  |  |
 | - | 0 | + |
 | 单调递减 |  | 单调递增 |
故
 的单调递减区间是
的单调递减区间是 ,间调递增区间是
,间调递增区间是
在
 处取得极小值,极小值为
处取得极小值,极小值为 6分
6分(2)设
 ,于是
,于是
由(1)知,当
 时,
时, 最小值为
最小值为
于是对任意的
 ,都有
,都有 ,所以
,所以 在
在 内单调递增.
内单调递增.于是当
 时,对任意
时,对任意
都有

而
 ,从而对任意
,从而对任意 ,
,
即:
 故,
故, 14分
14分
练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
 .其中
.其中 .
. 的值;
的值; ,若
,若 ,求
,求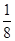 时,证明:方程f(x)=f
时,证明:方程f(x)=f 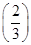 在区间(2,+∞)上有唯一解.
在区间(2,+∞)上有唯一解.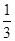 x3-ax2-ax,g(x)=2x2+4x+c.
x3-ax2-ax,g(x)=2x2+4x+c.

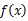 =
= 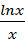 的最大值为( )
的最大值为( )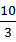
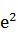

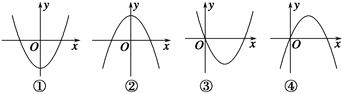
 x3+ax2+(a2-1)x+1(a∈R)的导函数y=f′(x)图象,则f(-1)等于________.
x3+ax2+(a2-1)x+1(a∈R)的导函数y=f′(x)图象,则f(-1)等于________.