题目内容
(原创)若对定义在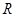 上的可导函数
上的可导函数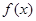 ,恒有
,恒有 ,(其中
,(其中 表示函数
表示函数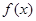 的导函数
的导函数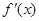 在
在 的值),则
的值),则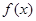 ( )
( )
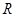 上的可导函数
上的可导函数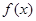 ,恒有
,恒有 ,(其中
,(其中 表示函数
表示函数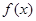 的导函数
的导函数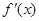 在
在 的值),则
的值),则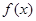 ( )
( )| A.恒大于等于0 | B.恒小于0 |
| C.恒大于0 | D.和0的大小关系不确定 |
C
试题分析:函数
 ,则
,则 =
= =
= =
= ,∵
,∵ 恒成立,∴当
恒成立,∴当 时,
时, ,此时函数
,此时函数 单调递增;当
单调递增;当 时,
时, ,此时函数
,此时函数 单调递减,∴当
单调递减,∴当 时,
时, 取得极小值,同时也是最小值
取得极小值,同时也是最小值 ,∴
,∴ ,即
,即 .当
.当 时,
时, ,∴当
,∴当 时,
时, .∵
.∵ 恒成立,∴当
恒成立,∴当 时,
时, 恒成立,∴
恒成立,∴ .综上无论
.综上无论 取何值,恒有
取何值,恒有 ,故选C.
,故选C.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
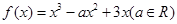 .
.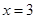 是
是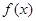 的极值点,求
的极值点,求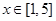 上的最大值;
上的最大值;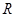 上的单调递增函数,求实数
上的单调递增函数,求实数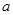 的取值范围.
的取值范围.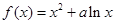 的图像在点
的图像在点 处的切线斜率为10.
处的切线斜率为10.  的值;
的值; 根的个数,并证明你的结论;
根的个数,并证明你的结论; ,使得曲线
,使得曲线 在该点附近的左、右两部分分别位于曲线在该点处切线的两侧? 若存在,求出点A的坐标;若不存在,说明理由.
在该点附近的左、右两部分分别位于曲线在该点处切线的两侧? 若存在,求出点A的坐标;若不存在,说明理由.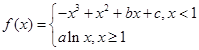 的图像过坐标原点
的图像过坐标原点 ,且在点
,且在点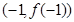 处的切线斜率为
处的切线斜率为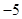 .
.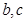 的值;
的值;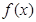 在区间
在区间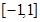 上的最小值;
上的最小值; 的图像上存在两点
的图像上存在两点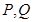 ,使得对于任意给定的正实数
,使得对于任意给定的正实数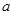 都满足
都满足 是以
是以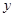 轴上,求点
轴上,求点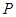 的横坐标的取值范围.
的横坐标的取值范围.

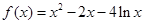 ,则
,则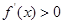 的解集为________.
的解集为________.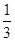 x3+ax2+(a2-1)x+1(a∈R)的导函数y=f′(x)图象,则f(-1)等于________.
x3+ax2+(a2-1)x+1(a∈R)的导函数y=f′(x)图象,则f(-1)等于________.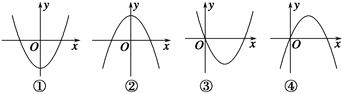
 x3+
x3+ x2-ax-a,x∈R,其中a>0.
x2-ax-a,x∈R,其中a>0.