题目内容
15.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{3}$=1(a>0)的一个焦点与抛物线y2=8x的焦点重合,则a=( )| A. | 1 | B. | 2 | C. | $\sqrt{13}$ | D. | $\sqrt{19}$ |
分析 根据题意,由抛物线的标准方程可得其焦点坐标,再结合双曲线的几何性质可得a2+b2=c2=4,计算可得a2的值,化简即可得答案.
解答 解:根据题意,抛物线的方程为y2=8x,其焦点在x轴正半轴上,且p=4,
则其焦点坐标为(2,0),
双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{3}$=1(a>0)的一个焦点为(2,0),即c=2,
则有a2+b2=c2=4,
又由b2=3,
则a2=c2-b2=1,
又由a>0,即a=1,
故选:A.
点评 本题考查双曲线、抛物线的几何性质,关键是由抛物线的标准方程,求出抛物线的焦点坐标.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
5.两千多年前,古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题.他们在沙滩上画点或用小石子表示数,按照点或小石子能排列的形状对数进行分类.如图中实心点的个数5,9,14,20,…为梯形数.根据图形的构成,记此数列的第2017项为a2017,则a2017-5=( )


| A. | 2023×2017 | B. | 2023×2016 | C. | 1008×2023 | D. | 2017×1008 |
6.一项针对人们休闲方式的调查结果如下:受调查对象总计124人,其中女性70人,男性54人.女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(1)根据以上数据建立一个2×2的列联表;
(2)根据下列提供的独立检验临界值表,你最多能有多少把握认为性别与休闲方式有关系?
独立检验临界值表:
参考公式:K2=$\frac{n(ad-bc)}{(a+b)(c+d)(a+c)(b+d)}$.
(1)根据以上数据建立一个2×2的列联表;
(2)根据下列提供的独立检验临界值表,你最多能有多少把握认为性别与休闲方式有关系?
独立检验临界值表:
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
20.已知函数f(x)=sin(ωx+φ)+1(ω>0,0≤φ≤$\frac{π}{2}$)的图象相邻两条对称轴之间的距离为π,且在x=$\frac{π}{3}$时取得最大值2,若f(α)=$\frac{8}{5}$,且$\frac{π}{3}$<α<$\frac{5π}{6}$,则sin(2α+$\frac{π}{3}$)的值为( )
| A. | $\frac{12}{25}$ | B. | -$\frac{12}{25}$ | C. | $\frac{24}{25}$ | D. | -$\frac{24}{25}$ |
5.互联网背景下的“懒人经济”和“宅经济”渐成声势,推动了互联网餐饮行业的发展,而“80后”、“90后”逐渐成为餐饮消费主力,年轻人的餐饮习惯的改变,使省时、高效、正规的外送服务逐渐进入消费者的视野,美团外卖为了调查市场情况,对50人进行了问卷调查得到了如下的列联表,按照出生年龄,对喜欢外卖与否,采用分成抽样的方法抽取容量为10的样本,则抽到喜欢外卖的人数为6.
(Ⅰ)请将下面的列联表补充完整:
(Ⅱ)能否在犯错误的概率不超过0.005的前提下认为喜欢外卖与年龄有关?说明你的理由;
(Ⅲ)把“80后”中喜欢外卖的10个消费者从2到11进行编号,从中抽取一人,先后两次抛掷一枚骰子,出现的点数之和为被抽取的序号,试求抽到6号或10号的概率.
下面的临界值表供参考:
(参考公式:K2=$\frac{{n(ad-bc)}^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
(Ⅰ)请将下面的列联表补充完整:
| 喜欢外卖 | 不喜欢外卖 | 合计 | |
| 90后 | 20 | 5 | 25 |
| 80后 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
(Ⅲ)把“80后”中喜欢外卖的10个消费者从2到11进行编号,从中抽取一人,先后两次抛掷一枚骰子,出现的点数之和为被抽取的序号,试求抽到6号或10号的概率.
下面的临界值表供参考:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

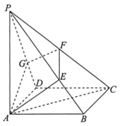 如图,在四棱锥P-ABCD中,底面ABCD为正方形,PA丄底面ABCD,PA=AC.过点A的平面与棱PB,PC,PD分别交于点E,F,G(E,F,G三点均不在棱的端点处).
如图,在四棱锥P-ABCD中,底面ABCD为正方形,PA丄底面ABCD,PA=AC.过点A的平面与棱PB,PC,PD分别交于点E,F,G(E,F,G三点均不在棱的端点处). 如图:三棱柱ABC-A1B1C1中,AA1⊥平面ABC,BC⊥AC,M是AB上的动点,CB=CA=CC1=2.
如图:三棱柱ABC-A1B1C1中,AA1⊥平面ABC,BC⊥AC,M是AB上的动点,CB=CA=CC1=2.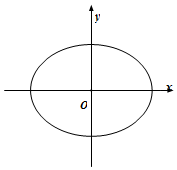 给定椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0).设t>0,过点T(0,t)斜率为k的 直线l与椭圆C交于M,N两点,O为坐标原点.
给定椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0).设t>0,过点T(0,t)斜率为k的 直线l与椭圆C交于M,N两点,O为坐标原点.