题目内容
设△ABC的外心为O,以线段OA、OB为邻边作平行四边形,第四个顶点为D,再以OC、OD为邻边作平行四边形,它的第四个顶点为H.(1)若
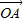 =
=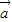 ,
,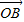 =
=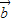 ,
,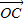 =
=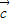 ,用
,用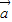 、
、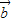 、
、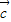 表示
表示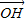 ;
;(2)求证:AH⊥BC;
(3)设△ABC中,∠A=60°,∠B=45°,外接圆半径为R,用R表示
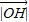 .(外心是三角形外接圆的圆心)
.(外心是三角形外接圆的圆心)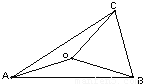
【答案】分析:(1)利用向量的三角形法则即可;
(2)利用向量的三角形法则、外心的性质、 ?
? 即可证明;
即可证明;
(3)利用向量模的计算公式、外心的性质即可求出.
解答:解:(1)由三角形法则可得 =
= =
= =
= ;
;
(2)∵ =
= =
= ,
, =
= ,
,
∴ =
= =
= ,
,
∵O点是△ABC的外心,∴ ,
,
∴ ,
,
∴ .即AH⊥BC
.即AH⊥BC
(3) =
= =
=
=
 ,
,
∵A=60°,点O是外心,∴ ,∴
,∴ ;
;
同理 =0,
=0, =
= .
.
∴ =
= .
.
∴ =
= =
= .
.
点评:熟练掌握三角形外心的性质、向量的三角形法则、 ?
? 及模的计算公式是解题的关键.
及模的计算公式是解题的关键.
(2)利用向量的三角形法则、外心的性质、
 ?
? 即可证明;
即可证明;(3)利用向量模的计算公式、外心的性质即可求出.
解答:解:(1)由三角形法则可得
 =
= =
= =
= ;
;(2)∵
 =
= =
= ,
, =
= ,
,∴
 =
= =
= ,
,∵O点是△ABC的外心,∴
 ,
,∴
 ,
,∴
 .即AH⊥BC
.即AH⊥BC(3)
 =
= =
=
=

 ,
,∵A=60°,点O是外心,∴
 ,∴
,∴ ;
;同理
 =0,
=0, =
= .
.∴
 =
= .
.∴
 =
= =
= .
.点评:熟练掌握三角形外心的性质、向量的三角形法则、
 ?
? 及模的计算公式是解题的关键.
及模的计算公式是解题的关键. 
练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
 设△ABC的外心为O,以线段OA、OB为邻边作平行四边形,第四个顶点为D,再以OC、OD为邻边作平行四边形,它的第四个顶点为H.
设△ABC的外心为O,以线段OA、OB为邻边作平行四边形,第四个顶点为D,再以OC、OD为邻边作平行四边形,它的第四个顶点为H. 设△ABC的外心为O,重心为G,取点H,使
设△ABC的外心为O,重心为G,取点H,使 设△ABC的外心为O(三角形外接圆的圆心),其外接圆半径为1,以线段OA、OB为邻边作平行四边形,第四个顶点为D,再以OC,OD为邻边作平行四边形,它的第四个顶点为H.若
设△ABC的外心为O(三角形外接圆的圆心),其外接圆半径为1,以线段OA、OB为邻边作平行四边形,第四个顶点为D,再以OC,OD为邻边作平行四边形,它的第四个顶点为H.若 设△ABC的外心为O,重心为G,取点H,使
设△ABC的外心为O,重心为G,取点H,使 .求证:
.求证: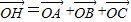 .求证:
.求证: