题目内容
设△ABC的外心为O（三角形外接圆的圆心），其外接圆半径为1，以线段OA、OB为邻边作平行四边形，第四个顶点为D，再以OC，OD为邻边作平行四边形，它的第四个顶点为H．若| OA |
| OB |
| OC |
（1）用a，b，c表示
| OH |
（2）求证：点H为△ABC的垂心；
（3）设△ABC中，∠A=60°，∠B=45°，求|
| OH |
分析：（1）利用向量的运算法则：三角形法则求出
（2）先将
用
，
，
表示，利用向量的数量积公式求出
•
，利用向量垂直的充要条件得到AH⊥BC，同理得到CH⊥AB，利用三角形垂心的定义得证
（3）利用向量的模的平方等于向量的平方及圆的圆周角等于圆心角的一半，利用向量的数量积公式，求出
的模，
| OH |
（2）先将
| AH |
| a |
| b |
| c |
| AH |
| BC |
（3）利用向量的模的平方等于向量的平方及圆的圆周角等于圆心角的一半，利用向量的数量积公式，求出
| OH |
解答：解：（1）
=
+
=
+(
+
)=
+
+
（2）
=
+
=-
+(
+
+
)=
+
=-
+
则
•
=(
+
)•(
-
=|
|2-|
|2
因为O为外心，且外接圆半径为1，所以|
|=|
|=1
∴
•
=|
|2-|
|2
则
⊥
，即AH⊥BC
同理可得：CH⊥AB
所以，点H为△ABC的垂心；
（3）|
|2=(
+
+
) 2=
2+
2+2
•
+2
•
+2
•
=1+1+1+2×1×1×cos∠AOB+2×1×1×cos∠BOC+2×1×1×cos∠COA=3+2（cos∠AOB+cos∠BOC+cos∠COA）
∵∠A=60°∴∠BOC=120°（圆心角是圆周角的两倍）
∴cos∠BOC=-
同理可得，cos∠AOC=0， cos∠AOB=-
∴|
|2=2-
∴|
|=
=
| OH |
| OC |
| OD |
| OC |
| OA |
| OB |
| a |
| b |
| c |
（2）
| AH |
| AO |
| OH |
| a |
| a |
| b |
| c |
| b |
| c |
| BC |
| b |
| c |
则
| AH |
| BC |
| b |
| c |
| c |
| b |
| c |
| b |
因为O为外心，且外接圆半径为1，所以|
| c |
| b |
∴
| AH |
| BC |
| c |
| b |
则
| AH |
| BC |
同理可得：CH⊥AB
所以，点H为△ABC的垂心；
（3）|
| OH |
| a |
| b |
| c |
| a2+ |
| b |
| c |
| a |
| b |
| b |
| c |
| c |
| a |
=1+1+1+2×1×1×cos∠AOB+2×1×1×cos∠BOC+2×1×1×cos∠COA=3+2（cos∠AOB+cos∠BOC+cos∠COA）
∵∠A=60°∴∠BOC=120°（圆心角是圆周角的两倍）
∴cos∠BOC=-
| 1 |
| 2 |
同理可得，cos∠AOC=0， cos∠AOB=-
| ||
| 2 |
∴|
| OH |
| 3 |
∴|
| OH |
2-
|
| ||||
| 2 |
点评：本题考查向量的运算法则、向量的数量积公式、向量垂直的充要条件、向量的模的平方等于向量的平方、圆的圆心角等于圆周角的二倍．
练习册系列答案
相关题目
设△ABC的外心为O，以线段OA、OB为邻边作平行四边形，第四个顶点为D，再以OC、OD为邻边作平行四边形，它的第四个顶点为H．
设△ABC的外心为O，重心为G，取点H，使
设△ABC的外心为O，重心为G，取点H，使
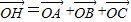．求证：
．求证：