题目内容
设△ABC的外心为O，重心为G，取点H，使
．求证：
（Ⅰ）点H为△ABC的垂心；
（Ⅱ）△ABC的外心O、重心G、垂心H在同一条直线上．
证明：（Ⅰ）∵O为△ABC的外心，∴
，
∵，∴
，
∴
∴
，即AH⊥BC，
同理BH⊥AC，CH⊥AB，
∴H为△ABC的垂心；
（Ⅱ）延长AG交BC于D，则D为BC中点，∴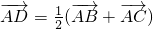
，
∵G为△ABC之重心，∴
∵
，
∴
，∴
，
∴O，G，H三点共线．
分析：（Ⅰ）根据O为△ABC的外心，可得，利用向量的加减法，向量的数量积，可证AH⊥BC，BH⊥AC，CH⊥AB，从而问题得证；
（Ⅱ）延长AG交BC于D，则D为BC中点，根据G为△ABC之重心，证明，即可得O，G，H三点共线．
点评：本题考查向量知识的运用，考查向量的数量积，考查向量共线，属于中档题．
，∵
，∴，∴
∴
，即AH⊥BC，同理BH⊥AC，CH⊥AB，
∴H为△ABC的垂心；
（Ⅱ）延长AG交BC于D，则D为BC中点，∴
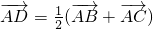，∵G为△ABC之重心，∴
∵
，∴
，∴，∴O，G，H三点共线．
分析：（Ⅰ）根据O为△ABC的外心，可得
，利用向量的加减法，向量的数量积，可证AH⊥BC，BH⊥AC，CH⊥AB，从而问题得证；（Ⅱ）延长AG交BC于D，则D为BC中点，根据G为△ABC之重心，证明
，即可得O，G，H三点共线．点评：本题考查向量知识的运用，考查向量的数量积，考查向量共线，属于中档题．
练习册系列答案
相关题目
设△ABC的外心为O，以线段OA、OB为邻边作平行四边形，第四个顶点为D，再以OC、OD为邻边作平行四边形，它的第四个顶点为H．
设△ABC的外心为O，重心为G，取点H，使
设△ABC的外心为O（三角形外接圆的圆心），其外接圆半径为1，以线段OA、OB为邻边作平行四边形，第四个顶点为D，再以OC，OD为邻边作平行四边形，它的第四个顶点为H．若
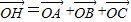．求证：