题目内容
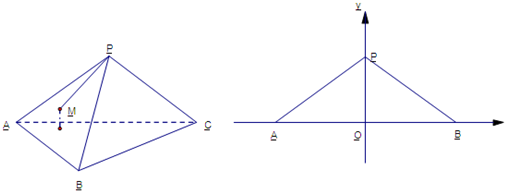
三棱锥P-ABC的底面为等腰直角三角形，∠C=90°，PC⊥AC，PC⊥BC，若PC=AC=4，则△ABP的面积为________．
分析：由于PC⊥AC，PC⊥BC，可知三棱锥P-ABC是正方体的一个角．△ABP是一个边长为4
的正三角形，在正△ABP中，求得△ABP的面积的大小即可．解答：
解：∵三棱锥P-ABC的底面为等腰直角三角形，∠C=90°，PC⊥AC，PC⊥BC，∴三棱锥P-ABC是正方体的一个角，
∴△ABP是一个边长为4
的正三角形，则△ABP的面积为
=
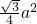=．故答案为：
．点评：本题以三棱锥为载体，考查空间想象能力，关键是得出△ABP是正三角形．
练习册系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
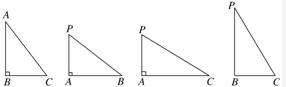13、下面一组图形为三棱锥P-ABC的底面与三个侧面．已知AB⊥BC，PA⊥AB，PA⊥AC．