Question

（2008•闵行区二模）已知正三棱锥P-ABC的底面边长为2

3

，体积为3

5

，则底面△ABC的中心O到侧面PAB的距离是

15

4

．

Answer 1

分析：由已知，可求出侧面PAB的面积，利用等体积法求出C到侧面PAB的距离，它是底面△ABC的中心O到侧面PAB的距离的3倍，利用此关系问题获解．

解答：解：如图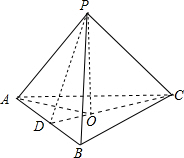设O为底面△ABC的中心，连接PO，连接CO并延长交AB于D，由正棱锥的性质，PO⊥底面△ABC，D为AB中点．CD=3
正△ABC的面积S=

3

4

AB2=3

3

，∵V=

1

3

S×PO=3

5

∴PO=

15

．OD=

1

3

CD=1，∴S△PAB=

1

2

AB×PD=4

3

，设C到面PAB的距离为h′，由VP-ABC=VC-PAB得

1

3

×4

3

h′=3

5

h′=

3 15

4

．又OD=

1

3

CD，∴O到侧面PAB的距离是

1

3

h′=

15

4

．
故答案为：

15

4

点评：本题考查空间点到平面的距离，利用等体积法进行转化求解．等体积是解决三棱锥中点面距的另一常见方法，此法的优点在于不必作出垂线段．