题目内容
已知f(x)=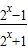 ,
,(1)求函数f(x)的定义域、值域.
(2)讨论f(x)的单调性.
【答案】分析:(1)对于任意实数x,都有2x>0,进而可得函数解析式恒有意义,即可得到函数f(x)的定义域;由f(x)=1-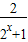 ,结合指数函数的值域利用分析法,可求出值域.
,结合指数函数的值域利用分析法,可求出值域.
(2)任取实数x1<x2,判断f(x1)-f(x2)的符号,进而根据函数单调性的定义,可得答案.
解答:解:(1)∵?x∈R,都有2x>0,
∴2x+1>1,
故函数f(x)=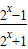 的定义域为实数集R.
的定义域为实数集R.
∵f(x)=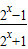 =1-
=1-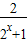 ,
,
而2x>0,
∴2x+1>1,
∴0<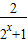 <2,
<2,
∴-2<-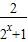 <0,
<0,
∴-1<1-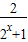 <1.
<1.
即-1<f(x)<1.
∴函数f(x)的值域为(-1,1).
(3)?x1<x2,
则f(x1)-f(x2)=1-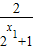 -(1-
-(1-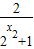 )=
)=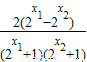 ,
,
∵2>1,∴2x1+1>0,2x2+1>0,2x1-2x2<0,
∴f(x1)<f(x2),
∴函数f(x)在实数集R上单调递增.
点评:本题综合考查了函数的定义域、值域及单调性,熟练掌握以上知识及方法是解决问题的关键.
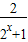 ,结合指数函数的值域利用分析法,可求出值域.
,结合指数函数的值域利用分析法,可求出值域.(2)任取实数x1<x2,判断f(x1)-f(x2)的符号,进而根据函数单调性的定义,可得答案.
解答:解:(1)∵?x∈R,都有2x>0,
∴2x+1>1,
故函数f(x)=
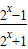 的定义域为实数集R.
的定义域为实数集R.∵f(x)=
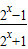 =1-
=1-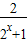 ,
,而2x>0,
∴2x+1>1,
∴0<
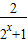 <2,
<2,∴-2<-
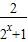 <0,
<0,∴-1<1-
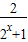 <1.
<1.即-1<f(x)<1.
∴函数f(x)的值域为(-1,1).
(3)?x1<x2,
则f(x1)-f(x2)=1-
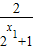 -(1-
-(1-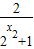 )=
)=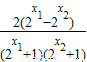 ,
,∵2>1,∴2x1+1>0,2x2+1>0,2x1-2x2<0,
∴f(x1)<f(x2),
∴函数f(x)在实数集R上单调递增.
点评:本题综合考查了函数的定义域、值域及单调性,熟练掌握以上知识及方法是解决问题的关键.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案
相关题目