题目内容
若双曲线的焦点为(0,4)和(0,-4),虚轴长为4
,则双曲线的方程为( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:根据双曲线的性质c2=a2+b2,由焦点,虚轴长是4
,分别求出半焦距c和半虚轴b,即可求出半实轴a的值,然后根据焦点在y轴上,从而求得的双曲线标准方程.
| 3 |
解答:解:根据题意可知2c=8,2b=4
,解得c=4,b=2
,根据双曲线的性质可得a2=c2-b2=4
又∵双曲线的焦点为(0,4)和(0,-4)
∴双曲线在y轴上
∴双曲线的标准方程为
-
=1
故选B
| 3 |
| 3 |
又∵双曲线的焦点为(0,4)和(0,-4)
∴双曲线在y轴上
∴双曲线的标准方程为
| y2 |
| 4 |
| x2 |
| 12 |
故选B
点评:此题考查学生掌握双曲线的性质,会利用待定系数法求双曲线的标准方程,是一道基础题.

练习册系列答案
相关题目
 ),虚轴长为
),虚轴长为 ,则双曲线的方程为(
).
,则双曲线的方程为(
).  B.
B. C.
C. D.
D.
 ,则双曲线的方程为
,则双曲线的方程为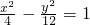
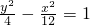
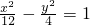

 ,则双曲线的方程为
,则双曲线的方程为 


