题目内容
如图,某园林单位准备绿化一块直径为BC的半圆形空地,△ABC外的地方种草,△ABC的内接正方形PQRS为一水池,其余的地方种花,若BC=a,∠ABC=θ,设△ABC的面积为S1,正方形的PQRS面积为S2.

(1)用a,θ表示S1和S2;
(2)当a固定,θ变化时,求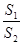 的最小值.
的最小值.

(1)用a,θ表示S1和S2;
(2)当a固定,θ变化时,求
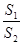 的最小值.
的最小值.(1)S1= a2sin 2θ,S2=
a2sin 2θ,S2= (2)
(2)
 a2sin 2θ,S2=
a2sin 2θ,S2= (2)
(2)
(1)S1= asin θ·acos θ=
asin θ·acos θ= a2sin 2θ,
a2sin 2θ,
设正方形边长为x,则BQ= ,RC=xtan θ,
,RC=xtan θ,
∴ +xtan θ+x=a,
+xtan θ+x=a,
∴x= ,(4分)
,(4分)
S2= ,(6分)
,(6分)
(2)当a固定,θ变化时,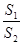 =
= ,
,
令sin 2θ=t,
则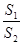 =
= (0<t≤1),
(0<t≤1),
利用单调性求得t=1时, min=
min= .(14分)
.(14分)
 asin θ·acos θ=
asin θ·acos θ= a2sin 2θ,
a2sin 2θ,设正方形边长为x,则BQ=
 ,RC=xtan θ,
,RC=xtan θ,∴
 +xtan θ+x=a,
+xtan θ+x=a,∴x=
 ,(4分)
,(4分) S2=
 ,(6分)
,(6分) (2)当a固定,θ变化时,
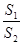 =
= ,
,令sin 2θ=t,
则
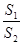 =
= (0<t≤1),
(0<t≤1),利用单调性求得t=1时,
 min=
min= .(14分)
.(14分)
练习册系列答案
相关题目
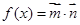 ,其中向量
,其中向量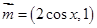 ,
,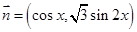 ,
,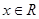 .
.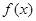 的单调递增区间;
的单调递增区间;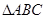 中,
中,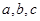 分别是角
分别是角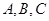 的对边,已知
的对边,已知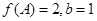 ,
,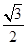 ,求
,求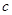 的值.
的值.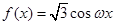 ,
,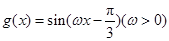 ,且
,且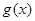 的最小正周期为
的最小正周期为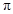 .
.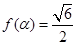 ,
,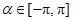 ,求
,求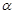 的值;
的值;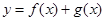 的单调增区间.
的单调增区间. .
. ,求
,求 的值;
的值; ,求
,求 的最大值.
的最大值. ;
; ,求
,求 的值.
的值.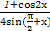 -asin
-asin cos(π-
cos(π-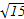

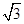 sin ωx+cos ωx(ω>0),y=f(x)的图象与直线y=2的两个相邻交点的距离等于π,则f(x)的单调递增区间是________.
sin ωx+cos ωx(ω>0),y=f(x)的图象与直线y=2的两个相邻交点的距离等于π,则f(x)的单调递增区间是________.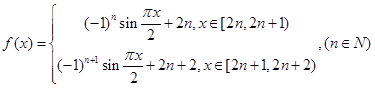 ,若数列
,若数列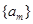 满足
满足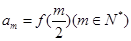 ,且
,且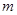 项和为
项和为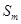 ,则
,则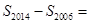 _____________.
_____________. 的值为________.
的值为________.