题目内容
如图,△ABC的顶点A(3,4)、B(6,0)、C(-5,-2),求∠A平分线AT所在的直线方程.
解法一:∵AC=![]() =10,AB=
=10,AB=![]() =5,∴T分
=5,∴T分![]() 所成比λ=
所成比λ=![]() =
= ![]() =2(三角形内角平分线性质).
=2(三角形内角平分线性质).
设T的坐标为(x,y),则x=![]() =
=![]() ,y=
,y=![]() =-
=-![]() .
.
∴T(![]() ,-
,-![]() ).
).
由直线方程的两点式得AT的方程为![]() =
=![]() ,即7x-y-17=0.
,即7x-y-17=0.
解法二:直线AC的斜率kAC=![]() =
=![]() ,直线AB的斜率kAB=
,直线AB的斜率kAB=![]() =-
=-![]() .
.
设直线AT的斜率为k(k>![]() ,或k<-
,或k<-![]()
![]() .∵直线AC到AT的角等于直线AT到AB的角,∴
.∵直线AC到AT的角等于直线AT到AB的角,∴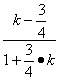 =
=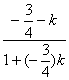 .
.
解得k=7或k=-![]() (舍去).
(舍去).
∴所求直线AT的方程为y-4=7(x-3),即7x-y-17=0.
解法三:由解法二知kAC·kAB=-1,即AC⊥AB.∵AT是∠A的平分线,∴∠CAT=45°.
设直线AT的斜率为k,得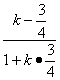 =tan45°=1,解得k=7.
=tan45°=1,解得k=7.
∴所求直线方程为y-4=7(x-3),即7x-y-17=0.
解法四:设直线AT上任一点P(x,y),则P点到直线AB、直线AC的距离相等.
直线AC方程为3x-4y+7=0,直线AB方程为4x+3y-24=0.
∴![]() =
=![]() .
.
化简,得x+7y-31=0或7x-y-17=0.
结合图形分析知x+7y-31=0为∠BAC的外角平分线方程,故舍去.
∴AT所在直线的方程为7x-y-17=0.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
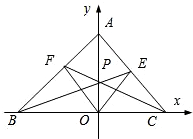 如图,在平面直角坐标系xoy中,设三角形ABC的顶点分别为A(0,a),B(b,0),C(c,0),点P(0,p)在线段AO上的一点(异于端点),这里a,b,c,p均为非零实数,设直线BP,CP分别与边AC,AB交于点E,F,某同学已正确求得直线OE的方程为
如图,在平面直角坐标系xoy中,设三角形ABC的顶点分别为A(0,a),B(b,0),C(c,0),点P(0,p)在线段AO上的一点(异于端点),这里a,b,c,p均为非零实数,设直线BP,CP分别与边AC,AB交于点E,F,某同学已正确求得直线OE的方程为 如图,已知△ABC的顶点坐标依次为A(1,0),B(5,8),C(7,-4),在边AB上有一点P,其横坐标为4,在AC上求一点Q,使线段PQ把△ABC分成面积相等的两部分.
如图,已知△ABC的顶点坐标依次为A(1,0),B(5,8),C(7,-4),在边AB上有一点P,其横坐标为4,在AC上求一点Q,使线段PQ把△ABC分成面积相等的两部分. 如图,直角△ABC的顶点A、B分别在x轴、y轴的正半轴上移动,直角顶点C与原点O在直线AB的两侧,则顶点C的轨迹是 ( )
如图,直角△ABC的顶点A、B分别在x轴、y轴的正半轴上移动,直角顶点C与原点O在直线AB的两侧,则顶点C的轨迹是 ( ) 如图,在坐标平面内△ABC的顶点A(0,2),B(-1,0),C(1,0),有一个随t变化的带形区域,其边界为直线y=t和y=t+1,设这个带形区域覆盖△ABC的面积为S,试求以t为自变量的函数S的解析式,并画出这个函数的图象.
如图,在坐标平面内△ABC的顶点A(0,2),B(-1,0),C(1,0),有一个随t变化的带形区域,其边界为直线y=t和y=t+1,设这个带形区域覆盖△ABC的面积为S,试求以t为自变量的函数S的解析式,并画出这个函数的图象.