Question

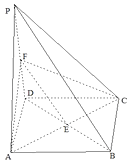
【题目】底面为正方形的四棱锥P﹣ABCD，F为PD中点．

（1）求证：PB∥面ACF；
（2）若PD⊥面ABCD，求证：AC⊥面PBD．

Answer 1

【答案】
（1）证明：∵四边形ABCD为正方形，

∴E为BD中点．

∵F为棱PD中点．

∴PB∥EF．

∵PB平面ACF，EF平面ACF，

∴直线PB∥平面ACF

（2）解：∵PD⊥面ABCD，AC平面ABCD，

∴PD⊥AC，

又∵正方形ABCD中，有AC⊥BD，且PD∩BD=D，

∴AC⊥面PBD．

【解析】（1）根据线面平行的判定定理证明PB∥EF即可证明PB∥平面EAC；（2）由PD⊥面ABCD，可证PD⊥AC，又可证AC⊥BD，利用线面垂直的判定定理即可证明AC⊥面PBD．
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识，掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行，以及对直线与平面垂直的判定的理解，了解一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想．