题目内容
【题目】在平面直角坐标系xOy中，点C在椭圆M： 
=1（a＞b＞0）上，若点A（﹣a，0），B（0， 
），且 
= 
．
（1）求椭圆M的离心率；
（2）设椭圆M的焦距为4，P，Q是椭圆M上不同的两点．线段PQ的垂直平分线为直线l，且直线l不与y轴重合．
①若点P（﹣3，0），直线l过点（0，﹣ 
），求直线l的方程；
②若直线l过点（0，﹣1），且与x轴的交点为D．求D点横坐标的取值范围．
【答案】
（1）解：设C（m，n），由 
= 
，
可得（a， 
a）= （m，n﹣ 
），
可得m= 
a，n= 
a，即C（ a， a），
即有 
+ 
=1，即为b2= a2，
c2=a2﹣b2= a2，
则e= 
=
（2）解：①由题意可得c=2，a=3，b= 
= 
，
即有椭圆方程为 
=1，
设直线PQ的方程为y=k（x+3），
代入椭圆方程可得（5+9k2）x2+54k2x+81k2﹣45=0，
x1+x2=﹣ 
，PQ的中点H为（﹣ 
， 
），
由题意可得直线l的斜率为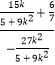 
=﹣ 
，
解得k=1或 ，
即有直线l的方程为y=﹣x﹣ 
或y=﹣ 
x﹣ ；
②设直线PQ的方程为y=kx+m，
代入椭圆方程可得，（5+9k2）x2+18kmx+9m2﹣45=0，
可得x1+x2=﹣ 
，
即有PQ的中点为（﹣ 
， 
），
由题意可得直线l的斜率为 
=﹣ ，
化简可得4m=5+9k2，中点坐标即为（﹣ 
， 
），
由中点在椭圆内，可得 
+ 
＜1，
解得﹣ 
＜k＜ ，
由直线l的方程为y=﹣ x﹣1，
可得D的横坐标为﹣k，可得范围是（﹣ ，0）∪（0， ）．
【解析】（1）设C（m，n），由向量共线的坐标表示，可得C的坐标，代入椭圆方程，可得a，b的关系，再由离心率公式计算即可得到所求值；（2）①由题意可得c=2，a=3，b= = ，可得椭圆方程，设直线PQ的方程为y=k（x+3），代入椭圆方程，运用韦达定理和中点坐标公式，再由两直线垂直的条件：斜率之积为﹣1，解方程可得k，进而得到所求直线方程；②设直线PQ的方程为y=kx+m，代入椭圆方程可得，运用韦达定理和中点坐标公式，再由两直线垂直的条件，求得4m=5+9k2 ， 再由中点在椭圆内，可得k的范围，再由直线l的方程可得D的横坐标的范围．
