题目内容
已知
在[0，1]上是
的减函数，则
的取值范围是 。
1＜
＜2
解析:
∵
是由
，
复合而成，又＞0
∴在[0，1]上是
的减函数，由复合函数关系知应为增函数，
∴＞1
又由于
在[0，1]上时 有意义，又是减函数，∴＝1时，取最小值是
＞0即可， ∴＜2
综上可知所求的取值范围是1＜＜2
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
已知
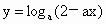在[0，1]上是x的减函数，则a的取值范围是
[
]|
A ．(0，1) |
B ．(1，2) |
|
C ．(0，2) |
D ．[2，＋∞) |
已知
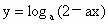在[0，1]上是关于x的减函数，则a的取值范围是
[
]|
A ．(0，1) |
B ．(1，2) |
|
C ．(0，2) |
D ．[2，＋∞) |
已知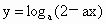
在[0，1]上是x的减函数，则a的取值范围是
[ ]
|
A．(0，1) |
B．(1，2) |
|
C．(0，2) |
D．[2，＋∞) |
已知
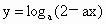在[0，1]上是减函数，则a的取值范围是
[
]|
A ．(0，1) |
B ．(1，2) |
|
C ．(0，2) |
D ．[2，＋∞) |
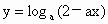在[0，1]上是关于x的减函数，则a的取值范围是