题目内容
无论a取何值,函数y=ax-2(a>0,且a≠1)的图象过定点A,而A在直线mx+ny-2=0上(m>0,n>0),则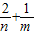 的最小值为 .
的最小值为 .
【答案】分析:依题意,可求得A(2,1),将其代入直线方程mx+ny-2=0,利用基本不等式即可求得 +
+ 的最小值.
的最小值.
解答:解:∵函数y=ax-2(a>0,且a≠1)的图象过定点A(2,1),
又点A(2,1)在直线mx+ny-2=0上(m>0,n>0),
∴2m+n=2,(m>0,n>0),
∴ +
+ =(
=( +
+ )•
)• (2m+n)=
(2m+n)= (
( +2+2+
+2+2+ )≥
)≥ ×(4+2
×(4+2 )=
)= (4+4)=4(当且仅当m=
(4+4)=4(当且仅当m= ,n=1时取“=”).
,n=1时取“=”).
∴ +
+ 的最小值为4.
的最小值为4.
故答案为:4.
点评:本题考查基本不等式,考查曲线恒过定点问题,考查转化与整体代入思想,属于中档题.
 +
+ 的最小值.
的最小值.解答:解:∵函数y=ax-2(a>0,且a≠1)的图象过定点A(2,1),
又点A(2,1)在直线mx+ny-2=0上(m>0,n>0),
∴2m+n=2,(m>0,n>0),
∴
 +
+ =(
=( +
+ )•
)• (2m+n)=
(2m+n)= (
( +2+2+
+2+2+ )≥
)≥ ×(4+2
×(4+2 )=
)= (4+4)=4(当且仅当m=
(4+4)=4(当且仅当m= ,n=1时取“=”).
,n=1时取“=”).∴
 +
+ 的最小值为4.
的最小值为4.故答案为:4.
点评:本题考查基本不等式,考查曲线恒过定点问题,考查转化与整体代入思想,属于中档题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 的最小值为________.
的最小值为________.