题目内容
已知椭圆C: ,两直线l1:x=-
,两直线l1:x=- ,l2:x=
,l2:x= ,直线l1为抛物线E:y2=16x的准线,直线l:x+2y-4=0与椭圆相切。
,直线l1为抛物线E:y2=16x的准线,直线l:x+2y-4=0与椭圆相切。
(Ⅰ)求椭圆C的方程;
(Ⅱ)如果椭圆C的左顶点为A,右焦点为F,过F的直线与椭圆C交于P,Q两点,直线AP,AQ与直线l2分别交于N,M两点,求证:四边形MNPQ的对角线的交点是定点。
 ,两直线l1:x=-
,两直线l1:x=- ,l2:x=
,l2:x= ,直线l1为抛物线E:y2=16x的准线,直线l:x+2y-4=0与椭圆相切。
,直线l1为抛物线E:y2=16x的准线,直线l:x+2y-4=0与椭圆相切。(Ⅰ)求椭圆C的方程;
(Ⅱ)如果椭圆C的左顶点为A,右焦点为F,过F的直线与椭圆C交于P,Q两点,直线AP,AQ与直线l2分别交于N,M两点,求证:四边形MNPQ的对角线的交点是定点。
(Ⅰ)解:由题知,抛物线y2=16x的准线方程为x=-4,
设椭圆 的右焦点为F(c,0),其中
的右焦点为F(c,0),其中 ,
,
则 ,即
,即 ,①
,①
由 ,消去x,得
,消去x,得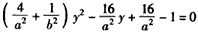 ,
,
由于直线x+2y-4=0与椭圆C相切,
所以
 ,
,
即4b2+a2-16=0,
所以4(a2-c2)+a2-16=0,
整理得5a2-4c2-16=0, ②
将①代人②,得5×4c-4c2-16=0,即c2-5c+4=0,解得c=1或4,
由于 ,所以c=1,
,所以c=1,
所以,所以椭圆C的方程为 。
。
(Ⅱ)证明:由(Ⅰ)知,A(-2,0),F(1,0),
直线l2的方程为x=4,
根据椭圆的对称性,当直线PQ⊥x轴时,四边形MNPQ是等腰梯形,对角线PM,ON的交点在x轴上,
此时,直线PQ的方程为x=1,
由 ,得
,得 ,
,
不妨取 ,故直线AP的方程为
,故直线AP的方程为 ,
,
将x=4代入,得N(4,3),所以,直线QN的方程为 ,
,
令y=0,得x=2,即直线QN与x轴的交点为R(2,0),
此点恰为椭圆的右顶点.
下面只要证明,在一般情况下Q,N,R三点共线即可.
设P(x1,y1),Q(x2,y2),N(4,y3),M(4,y4),直线PQ的方程为x=my+1,
由 消去x,得
消去x,得 ,
,
所以,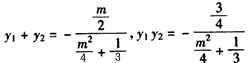 ,
,
因为 三点共线,
三点共线,
所以, 与
与 共线,
共线,
所以 ,即
,即 ,
,
由于, ,
,
所以,

所以, 共线,即Q,N,R三点共线。
共线,即Q,N,R三点共线。
同理可证,P,M,R三点共线。
所以,四边形MNPQ的对角线的交点是定点,此定点恰为椭圆的右顶点。

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
 的两个焦点是F1(
的两个焦点是F1( c,0),F2(c,0)(c>0)。
c,0),F2(c,0)(c>0)。 与椭圆C有公共点,求
与椭圆C有公共点,求 的取值范围;
的取值范围; 且
且 ,其中N为椭圆的下顶点,求直线l在y轴上截距的取值范围.
,其中N为椭圆的下顶点,求直线l在y轴上截距的取值范围. 的两个焦点为F1、F2,点P在椭圆C上,且|PF1|=
的两个焦点为F1、F2,点P在椭圆C上,且|PF1|= ,
, , PF1⊥F1F2.
, PF1⊥F1F2.  的两个焦点为
的两个焦点为 、
、
 ,且经过点
,且经过点 ,一组斜率为
,一组斜率为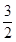 的直线与椭圆C都相交于不同两点
的直线与椭圆C都相交于不同两点 、
、 。
。 的中点都有在同一直线
的中点都有在同一直线 上;
上; MNQ面积为
MNQ面积为 的点Q有几个?证明你的结论。(不必具体求出Q点的坐标)
的点Q有几个?证明你的结论。(不必具体求出Q点的坐标)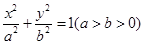 ,两个焦点分别为
,两个焦点分别为 、
、 ,斜率为k的直线
,斜率为k的直线 过右焦点
过右焦点 的中点恰为B。
的中点恰为B。 ,求椭圆C的离心率的取值范围。
,求椭圆C的离心率的取值范围。 ,A、B到右准线距离之和为
,A、B到右准线距离之和为 ,求椭圆C的方程。
,求椭圆C的方程。