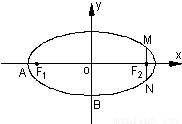
题目内容
已知椭圆C: 的两个焦点为
的两个焦点为 、
、
 ,且经过点
,且经过点 ,一组斜率为
,一组斜率为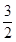 的直线与椭圆C都相交于不同两点
的直线与椭圆C都相交于不同两点 、
、 。
。
(1)求椭圆C的方程;
(2)证明:线段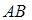 的中点都有在同一直线
的中点都有在同一直线 上;
上;
(3)对于(2)中的直线 ,设
,设 与椭圆C交于两点M、N,试探究椭圆上使
与椭圆C交于两点M、N,试探究椭圆上使 MNQ面积为
MNQ面积为 的点Q有几个?证明你的结论。(不必具体求出Q点的坐标)
的点Q有几个?证明你的结论。(不必具体求出Q点的坐标)
【答案】
解:(1)(法一)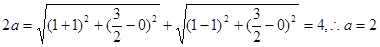
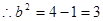
 椭圆C的方程为
椭圆C的方程为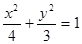
(法二)由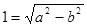 ,
,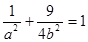 解得
解得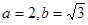
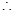 椭圆C的方程为
椭圆C的方程为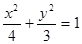
(2)(法一)设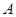
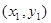 、
、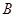
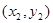 ,
,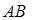 的中点坐标
的中点坐标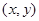 ,则
,则
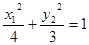 ,
,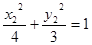 两式相减得
两式相减得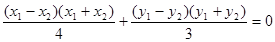
又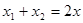 ,
,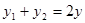 ,
, 代入,得
代入,得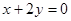
 线段
线段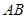 的中点都有在同一直线
的中点都有在同一直线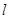 :
: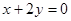 上;
上;
(法二)设直线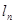 的方程为
的方程为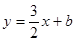 ,代入
,代入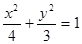 得
得
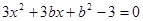 ,设
,设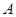
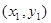 、
、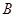
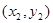 ,
,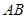 的中点坐标
的中点坐标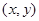 ,则
,则
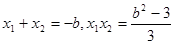 ,则
,则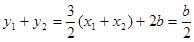
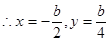 消去
消去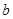 得
得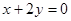
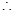 线段
线段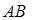 的中点都有在同一直线
的中点都有在同一直线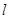 :
: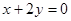 上;(中点弦、定直线、消参求轨迹)
上;(中点弦、定直线、消参求轨迹)
(3)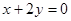 代入
代入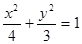 得
得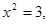
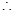
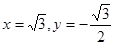 或
或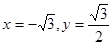
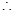 |MN|=
|MN|=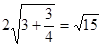 ,
,
设点Q到直线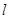 的距离为
的距离为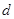 ,则由
,则由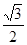 =
=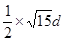 得
得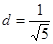
(法一)设Q在与直线MN平行的直线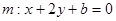 上,则直线
上,则直线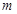 与直线MN的距离为
与直线MN的距离为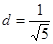
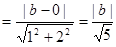 解得
解得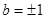 ,
,
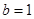 时,
时,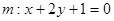 代入
代入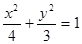 得
得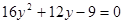 ①
①
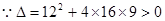 ,
,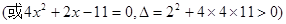
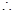 方程①有两不等实解,即有两个不同点Q满足;同理可得,
方程①有两不等实解,即有两个不同点Q满足;同理可得,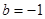 时也有两个不同的点Q满足。
时也有两个不同的点Q满足。
综上,共有4个不同点Q满足条件
(若求点Q坐标,则为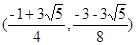
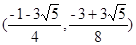
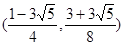
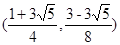 )
)
法(二)设D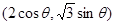 为椭圆上不同于M、N的任一点,D到MN的距离为
为椭圆上不同于M、N的任一点,D到MN的距离为
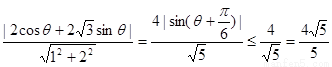 ,
,
即椭圆C上点到直线MN距离的最大值为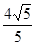 ,
,
而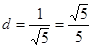
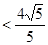 ,故由图可知,椭圆C上有4个点Q能满足条件。
,故由图可知,椭圆C上有4个点Q能满足条件。
【解析】略

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 如图,在直角坐标系xOy中,已知椭圆C:
如图,在直角坐标系xOy中,已知椭圆C: +
+ =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的
,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的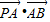 =m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.
=m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.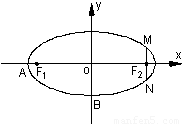
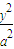 +
+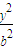 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=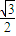 ,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的
,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的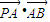 =m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.
=m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.