题目内容
已知椭圆C: 的两个焦点是F1(
的两个焦点是F1( c,0),F2(c,0)(c>0)。
c,0),F2(c,0)(c>0)。
(I)若直线 与椭圆C有公共点,求
与椭圆C有公共点,求 的取值范围;
的取值范围;
(II)设E是(I)中直线与椭圆的一个公共点,求|EF1|+|EF2|取得最小值时,椭圆的方程;
(III)已知斜率为k(k≠0)的直线l与(II)中椭圆交于不同的两点A,B,点Q满足  且
且 ,其中N为椭圆的下顶点,求直线l在y轴上截距的取值范围.
,其中N为椭圆的下顶点,求直线l在y轴上截距的取值范围.
【答案】
(I)  .(II)
.(II) .(III)直线
.(III)直线 纵截距的范围是
纵截距的范围是 .
.
【解析】
试题分析:(I)由题意联立方程组
由 得
得 ,
,
根据 ,即可得到
,即可得到 的取值范围是
的取值范围是 .
.
(II)由椭圆的定义得 ,
,
及 ,得到当
,得到当 时,
时, 有最小值
有最小值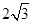 ,确定得到椭圆的方程的方程.
,确定得到椭圆的方程的方程.
(III)设直线方程为 ,
,
通过联立 ,整理得到一元二次方程,设
,整理得到一元二次方程,设 ,
,
应用韦达定理,结合 得
得 为
为 的中点,
的中点,
 ,得到
,得到 ,可建立
,可建立 的方程,
从而由
的方程,
从而由 得到
得到 使问题得解.
使问题得解.
试题解析:(I)由题意知 .
.
由 得
得 ,
,
所以 ,解得
,解得 ,
,
所以求 的取值范围是
的取值范围是 .
.
(II)由椭圆的定义得 ,
,
因为 ,所以当
,所以当 时,
时, 有最小值
有最小值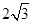 ,
,
此时椭圆的方程的方程为 .
.
(III)设直线方程为 ,
,
由 整理得
整理得 ,
,
化简得
设
则
由 得
得 为
为 的中点,所以
的中点,所以
因为 ,所以
,所以
即 ,化简得
,化简得
又 ,
,
所以
又 ,所以
,所以
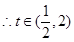 .
.
考点:椭圆的定义、标准方程,直线与椭圆的位置关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
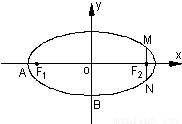
 如图,在直角坐标系xOy中,已知椭圆C:
如图,在直角坐标系xOy中,已知椭圆C: +
+ =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的
,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的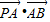 =m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.
=m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.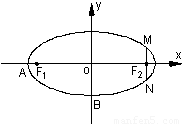
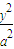 +
+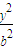 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=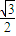 ,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的
,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的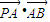 =m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.
=m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.