题目内容
8.已知奇函数f(x)=$\left\{\begin{array}{l}-{x^2}+2x(x>0)\\ 0,(x=0)\\{x^2}+mx(x<0)\end{array}$(1)在给出的直角坐标系中画出y=f(x)的图象,并求实数m的值;
(2)若函数f(x)在区间[2a-1,a+1]上单调递增,试确定a的取值范围.
分析 (1)当 x<0时,-x>0,结合f(x)为奇函数,f(-x)=-f(x),可得m值,结合二次函数的图象,可得y=f(x)的图象;
(2)由(1)知f(x),由图象可知,f(x)在[-1,1]上单调递增,要使f(x)在[2a-1,a+1]上单调递增,只需$\left\{\begin{array}{l}a+1>2a-1\\ a+1≤1\\ 2a-1≥-1\end{array}\right.$,解得答案.
解答 解:(1)当 x<0时,
-x>0,f(-x)=-(x)2+2(-x)=-x2-2x
又f(x)为奇函数,
∴f(-x)=-f(x)=-x2-2x,
∴f(x)=x2+2x,
∴m=2
y=f(x)的图象如图所示: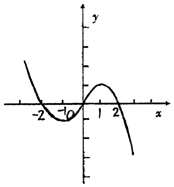
(2)由(1)知f(x),
由图象可知,f(x)在[-1,1]上单调递增,
要使f(x)在[2a-1,a+1]上单调递增,
只需$\left\{\begin{array}{l}a+1>2a-1\\ a+1≤1\\ 2a-1≥-1\end{array}\right.$
解之得:a=0.
点评 本题考查的知识点是分段函数的应用,数形结合思想,二次函数的图象和性质,难度中档.

练习册系列答案
相关题目
16.集合A={-1,1},B={x|mx=1},A∪B=A,则实数m组成的集合( )
| A. | {-1} | B. | {1} | C. | {-1,1} | D. | {-1,0,1} |
3.在正四棱锥P-ABCD中,O为正方形ABCD的中心,$\overrightarrow{PE}$=λ$\overrightarrow{EO}$(2≤λ≤4),且平面ABE与直线PD交于F,$\overrightarrow{PF}$=f(λ)$\overrightarrow{PD}$,则( )
| A. | f(λ)=$\frac{λ}{λ+2}$ | B. | f(λ)=$\frac{2λ}{λ+6}$ | C. | f(λ)=$\frac{3λ}{λ+7}$ | D. | f(λ)=$\frac{4λ}{λ+9}$ |
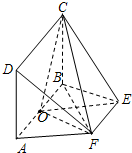 如图,AB为圆O的直径,点E、F在圆O上,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.
如图,AB为圆O的直径,点E、F在圆O上,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.