题目内容
如题(20)图,三棱锥P-ABC中,平面PAC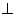 平面ABC,
平面ABC,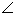 ABC=
ABC=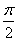 ,点D、E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF//BC.
,点D、E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF//BC.
证明:AB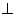 平面PFE.
平面PFE.
若四棱锥P-DFBC的体积为7,求线段BC的长.

证明:如题(20)图.由DE=EC,PD=PC知,E为等腰 PDC中DC边的中点,故
PDC中DC边的中点,故
PE  AC,
AC,

又平面PAC  平面ABC,平面PAC
平面ABC,平面PAC  平面ABC=AC,PE
平面ABC=AC,PE  平面PAC,PE
平面PAC,PE  AC,所以PE
AC,所以PE  平面ABC,从而PE
平面ABC,从而PE  AB.
AB.
因 .
.
从而AB与平面PEF内两条相交直线PE,EF都垂直,
所以 平面PFE.
平面PFE.
(2)解:设 ,则在直角
,则在直角 ABC中,
ABC中,
 .从而
.从而
由 ,知
,知 ,得
,得 ,故
,故 ,
,
即 .
.
由 ,
, ,
,
从而四边形DFBC的面积为

由(1)知,PE  平面ABC,所以PE为四棱锥P-DFBC的高.
平面ABC,所以PE为四棱锥P-DFBC的高.
在直角 中,
中, ,
,
体积 ,
,
故得 ,解得
,解得 ,由于
,由于 ,可得
,可得 .
.
所以 .
.

练习册系列答案
相关题目
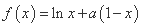 .
. 的单调性;
的单调性;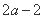 时,求a的取值范围.
时,求a的取值范围. 的展开式中x的奇数次幂项的系数之和为32,则α=__________.
的展开式中x的奇数次幂项的系数之和为32,则α=__________. (B)
(B)  (C)
(C)  (D)
(D) 

 上随机地选择一个数p,则方程
上随机地选择一个数p,则方程 有两个负根的概率为________.
有两个负根的概率为________.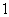 B.
B.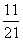 C.
C.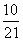 D.
D.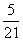
 ,则b=___
,则b=___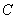 :
: 的离心率
的离心率 ,且其右焦点
,且其右焦点 ,则双曲线
,则双曲线 B.
B.  C.
C.  D.
D. 
 C. 2 D.
C. 2 D. 