题目内容
袋中共有15个除了颜色外完全相同的球,其中有10个白球,5个红球,从袋中任取2个球,所取的2个球中恰有一个白球,1个红球的概率为
A.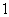 B.
B.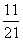 C.
C.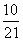 D.
D.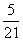
C

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
题目内容
袋中共有15个除了颜色外完全相同的球,其中有10个白球,5个红球,从袋中任取2个球,所取的2个球中恰有一个白球,1个红球的概率为
A.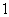 B.
B.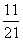 C.
C.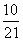 D.
D.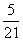
C

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案