题目内容
已知{an}为等差数列，若a3+a4+a8=9，则a5=（ ）
| A、3 | B、4 | C、5 | D、6 |
考点：等差数列的通项公式
专题：等差数列与等比数列
分析：由等差数列的性质易得3a4=9，解之可得．
解答：
解：由等差数列的性质可得a3+a4+a8=a3+a8+a4=a5+a6+a4=3a5，
又a3+a4+a8=9，∴3a5=9，解得a5=3
故选：A
又a3+a4+a8=9，∴3a5=9，解得a5=3
故选：A
点评：本题考查等差数列的性质和通项公式，属基础题．
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
小学期末标准试卷系列答案
相关题目
若角α和角β的终边关于x轴对称，则角α可以用角β表示为（ ）
| A、K•360°+β（k∈Z） |
| B、K•360°-β（k∈Z） |
| C、K•180°+β（k∈Z） |
| D、K•180°-β（k∈Z） |
复数-
的共轭复数是（ ）
| 1+i |
| i |
| A、1-i | B、-1+i |
| C、1+i | D、-1-i |
设全集U={1，2，3，4，5，6，7，8}，A={1，2，3}，B={3，4，5，6}，则A∩（∁UB）=（ ）
| A、{1，2，3} |
| B、{1，2} |
| C、{1，3} |
| D、{1} |
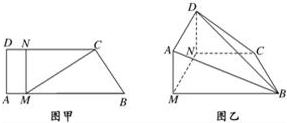如图甲，直角梯形ABCD中，AB∥CD，∠ADC=90°，点M，N分别在线段AB、CD上，且MN⊥AB，BC=1，MB=2，∠CBM=60°，若梯形ABCD沿MN折起，使DN⊥NC，如图乙．