��Ŀ����
5�� ��ͼ����֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0������ΪF����PΪ��ԲC������һ�㣬��|PF|����СֵΪ$\sqrt{2}$-1��������Ϊ$\frac{\sqrt{2}}{2}$��ֱ��l����ԲC���ڲ�ͬ����A��B��A��B����x���Ϸ������ҡ�OFA+��OFB=180�㣮
��ͼ����֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0������ΪF����PΪ��ԲC������һ�㣬��|PF|����СֵΪ$\sqrt{2}$-1��������Ϊ$\frac{\sqrt{2}}{2}$��ֱ��l����ԲC���ڲ�ͬ����A��B��A��B����x���Ϸ������ҡ�OFA+��OFB=180�㣮��������ԲC�ķ��̣�
����AΪ��Բ��y��������Ľ���ʱ����ֱ��l�ķ��̣�
�����ڶ�ֱ��l���Ƿ����һ�����㣬���ۡ�OFA��α仯��ֱ��l�ܾ����˶��㣿�����ڣ�����ö�������ꣻ�������ڣ���˵�����ɣ�
���� ��������Բ�ı�����Ϊ��$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0������������Ϊ$\frac{\sqrt{2}}{2}$����PΪ��ԲC������һ�㣬��|PF|����СֵΪ$\sqrt{2}$-1�����a2=2��b2=1���ɴ��������ԲC�ķ��̣�
����������A��0��1����F��-1��0������kAF=$\frac{1-0}{0-��-1��}$=1���Ӷ�kBF=-1������ֱ��BFΪ��y=-x-1������$\frac{{x}^{2}}{2}+{y}^{2}=1$����3x2+4x=0���ɴ������ֱ��AB�ķ��̣�
�����ɡ�OFA+��OFB=180�㣬֪B����x��ĶԳƵ�B1��ֱ��AF�ϣ���ֱ��AF�ķ���Ϊ��y=k��x+1������$\left\{\begin{array}{l}{y=k��x+1��}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$���ã�${k}^{2}+\frac{1}{2}$��x2+2k2x+k2-1=0���ɴ�����Τ�ﶨ����ֱ�ߵ�б�ʡ�ֱ�߷��̣������֪������������ڶ�ֱ��l������һ������M��-2��0�������ۡ�OFA��α仯��ֱ��l�ܾ����˶��㣮
��� �⣺��������Բ�ı�����Ϊ��$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����
��������Ϊ$\frac{\sqrt{2}}{2}$����${e}^{2}=\frac{{c}^{2}}{{a}^{2}}=\frac{{a}^{2}-{b}^{2}}{{a}^{2}}=\frac{1}{2}$����a=$\sqrt{2}b$��
�ߵ�PΪ��ԲC������һ�㣬��|PF|����СֵΪ$\sqrt{2}$-1��
��c=1����a2=b2+c2=b2+1��
���a2=2��b2=1��
����ԲC�ķ���Ϊ$\frac{{x}^{2}}{2}+{y}^{2}$=1��
����������A��0��1����F��-1��0����
��kAF=$\frac{1-0}{0-��-1��}$=1��
�ߡ�OFA+��OFB=180�㣮��kBF=-1��
��ֱ��BFΪ��y=-��x+1��=-x-1��
����$\frac{{x}^{2}}{2}+{y}^{2}=1$����3x2+4x=0�����x=0��x=-$\frac{4}{3}$��
����y=-x-1����$\left\{\begin{array}{l}{x=0}\\{y=-1}\end{array}\right.$���ᣬ��$\left\{\begin{array}{l}{x=-\frac{4}{3}}\\{y=\frac{1}{3}}\end{array}\right.$����B��-$\frac{4}{3}$��$\frac{1}{3}$����
��${k}_{AB}=\frac{1-\frac{1}{3}}{0-��-\frac{4}{3}��}$=$\frac{1}{2}$����ֱ��AB�ķ���Ϊ��y=$\frac{1}{2}x+1$��
������һ������M��-2��0�������ۡ�OFA��α仯��ֱ��l�ܾ����˶��㣮
֤�����ߡ�OFA+��OFB=180�㣬��B����x��ĶԳƵ�B1��ֱ��AF�ϣ�
��ֱ��AF�ķ���Ϊ��y=k��x+1����
����$\left\{\begin{array}{l}{y=k��x+1��}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$���ã�${k}^{2}+\frac{1}{2}$��x2+2k2x+k2-1=0��
��Τ�ﶨ����${x}_{1}+{x}_{2}=\frac{2{k}^{2}}{{k}^{2}+\frac{1}{2}}$��${x}_{1}{x}_{2}=\frac{{k}^{2}-1}{{k}^{2}+\frac{1}{2}}$��
��ֱ��AB��б��${k}_{AB}=\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$����AB�ķ���Ϊ��y-y1=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$��x-x1��
��y=0���ã�
x=x1-y1•$\frac{{x}_{1}-{x}_{2}}{{y}_{1}-{y}_{2}}=\frac{{x}_{2}{y}_{1}-{x}_{1}{y}_{2}}{{y}_{1}-{y}_{2}}$��
y1=k��x1+1����-y2=k��x2+1����
$x=\frac{{x}_{2}{y}_{1}-{x}_{1}{y}_{2}}{{y}_{1}-{y}_{2}}$=$\frac{{x}_{2}��k��{x}_{1}+1��+{x}_{1}��k��{x}_{2}+1��}{k��{x}_{1}+1��+k��{x}_{2}+1��}$=$\frac{2{x}_{1}{x}_{2}+{x}_{1}+{x}_{2}}{{x}_{1}+{x}_{2}+2}$
=��$\frac{2��\frac{{k}^{2}-1}{{k}^{2}+\frac{1}{2}}-\frac{2{k}^{2}}{{k}^{2}+\frac{1}{2}}}{2-\frac{2{k}^{2}}{{k}^{2}+\frac{1}{2}}}$=-2��
����ڶ�ֱ��l������һ������M��-2��0�������ۡ�OFA��α仯��ֱ��l�ܾ����˶��㣮
���� ���⿼����Բ���̵�������ֱ�߷��̵�������ֱ���Ƿ��������ж��������е��⣬����ʱҪ�������⣬ע����Բ���ʵĺ������ã�

 ������ȫ�̼����ĩ���100��ϵ�д�
������ȫ�̼����ĩ���100��ϵ�д�| A�� | 2��3 | B�� | 4��3 | C�� | 5��3 | D�� | 8��3 |
| A�� | ��$\frac{1}{4}$��1�� | B�� | ��1��4�� | C�� | ��1��8�� | D�� | ��8��+�ޣ� |
| A�� | 1 | B�� | -1 | C�� | ��1 | D�� | 3 |
 ��Բ$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1��{a��b��0}��$��������ΪA��B��ͼ��������Ϊ$\frac{{\sqrt{2}}}{2}$�����佹��F��0��1����ֱ��l����Բ����C��D���㣬����x�ύ�ڵ�P��ֱ��AC��ֱ��BD���ڵ�Q��
��Բ$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1��{a��b��0}��$��������ΪA��B��ͼ��������Ϊ$\frac{{\sqrt{2}}}{2}$�����佹��F��0��1����ֱ��l����Բ����C��D���㣬����x�ύ�ڵ�P��ֱ��AC��ֱ��BD���ڵ�Q��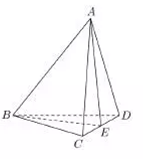 ��ͼ������A-BCD�У���BCDΪ�ȱ������Σ�AC=AD��EΪCD���е㣻
��ͼ������A-BCD�У���BCDΪ�ȱ������Σ�AC=AD��EΪCD���е㣻