题目内容
已知函数f(x)=ln x-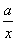 .
.
(1)若a>0,试判断f(x)在定义域内的单调性;
(2)若f(x)<x2在(1,+∞)上恒成立,求a的取值范围.
【解】(1)由题意知f(x)的定义域为(0,+∞),且f′(x)=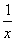 +
+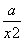 =
=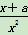 .
.
∵a>0,∴f′(x)>0,故f(x)在(0,+∞)上是单调递增函数.
(2)∵f(x)<x2,∴ln x-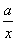 <x2.又x>0,∴a>xln x-x3.
<x2.又x>0,∴a>xln x-x3.
令g(x)=xln x-x3,h(x)=g′(x)=1+ln x-3x2,
h′(x)=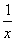 -6x=
-6x=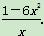
∵x∈(1,+∞)时,h′(x)<0,
∴h(x)在(1,+∞)上是减函数.∴h(x)<h(1)=-2<0,即g′(x)<0,∴g(x)在(1,+∞)上也是减函数.
g(x)<g(1)=-1,∴当a≥-1时,f(x)<x2在(1,+∞)上恒成立.
那a的取值范围是[-1,+∞).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 .若关于
.若关于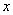 的方程
的方程 有两个
有两个 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
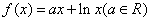 .
. 的单调区间;(2)设
的单调区间;(2)设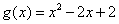 ,若对任意
,若对任意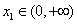 ,均存在
,均存在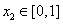 ,使得
,使得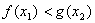 ,求
,求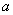 的取值范围.
的取值范围. .
. 处的切线方程;(2)求曲线过点
处的切线方程;(2)求曲线过点 ,在
,在 时的速度为 .
时的速度为 . ,讨论
,讨论 的单调性.
的单调性. 是首项为1,公差为2的等差数列,
是首项为1,公差为2的等差数列, 表示
表示 项和.
项和. 及
及 是首项为2的等比数列,公比
是首项为2的等比数列,公比 满足
满足 ,求
,求 .
.