题目内容
已知 是首项为1,公差为2的等差数列,
是首项为1,公差为2的等差数列, 表示
表示 的前
的前 项和.
项和.
(1)求 及
及 ;
;
(2)设 是首项为2的等比数列,公比
是首项为2的等比数列,公比 满足
满足 ,求
,求 的通项公式及其前
的通项公式及其前 项和
项和 .
.
解:(1)因为{an}是首项a1=1,公差d=2的等差数列,所以
an=a1+(n-1)d=2n-1.
故Sn=1+3+…+(2n-1)= =
= =n2.
=n2.
(2)由(1)得a4=7,S4=16.因为q2-(a4+1)q+S4=0,即q2-8q+16=0,
所以(q-4)2=0,从而q=4.
又因为b1=2,{bn}是公比q=4的等比数列,
所以bn=b1qn-1=2×4n-1=22n-1.
从而{bn}的前n项和Tn= =
= (4n-1).
(4n-1).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
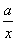 .
. 在
在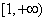 上是单调增函数,则
上是单调增函数,则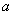 的最大值是( )
的最大值是( ) B.
B. C.
C. D.
D.
 满足
满足 ,求
,求
 ,则该数列的公差
,则该数列的公差 ( )
( ) 为数列
为数列 的前
的前 项和,已知
项和,已知 ,
, ,
, .(1)求
.(1)求 ,
, ,并求数列
,并求数列 的前
的前 中,
中, ,
, ,
, ,那么数列
,那么数列 的前
的前 项和等于( )
项和等于( ) B.
B. C.
C. D.
D.
 的通项公式为
的通项公式为 , 则
, 则
 满足
满足 ,则数列
,则数列 的前
的前 项的和等于( )
项的和等于( ) B.
B. C.
C. D.
D.