题目内容
函数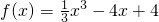 在区间[-3,4]上的最小值为
在区间[-3,4]上的最小值为
- A.

- B.-12
- C.

- D.-9
C
分析:先对函数f(x)进行求导,然后令导函数等于0求出x的值,然后判断端点值和极值的大小进而得到最小值.
解答:∵f'(x)=4-x2,
∴f'(x)=0,得x=±2,
∵f(-3)=7,f(-2)= ,f(2)=-
,f(2)=- ,f(4)=
,f(4)= ,
,
∴f(x)min=f(2)=- .
.
故选C.
点评:本题主要考查函数在闭区间上的最值.利用导数求函数在闭区间上的最值是一种常用的方法,要熟练掌握.
分析:先对函数f(x)进行求导,然后令导函数等于0求出x的值,然后判断端点值和极值的大小进而得到最小值.
解答:∵f'(x)=4-x2,
∴f'(x)=0,得x=±2,
∵f(-3)=7,f(-2)=
 ,f(2)=-
,f(2)=- ,f(4)=
,f(4)= ,
,∴f(x)min=f(2)=-
 .
.故选C.
点评:本题主要考查函数在闭区间上的最值.利用导数求函数在闭区间上的最值是一种常用的方法,要熟练掌握.

练习册系列答案
相关题目
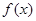 满足:
满足: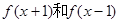 都是偶函数,当
都是偶函数,当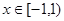 时
时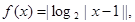 ,则下列说法错误的是( )
,则下列说法错误的是( )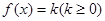 在
在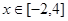 上一定有偶数个解;
上一定有偶数个解;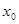 ,且
,且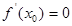
 .
.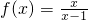 在(1,+∞)上是单调减函数;
在(1,+∞)上是单调减函数; 在区间[-3,4]上的最小值为( )
在区间[-3,4]上的最小值为( )

 在区间[3,4]上是单调递减函数,则实数a的取值范围为
在区间[3,4]上是单调递减函数,则实数a的取值范围为

