题目内容
已知函数![]() 图像上一点
图像上一点![]() 处的切线方程为
处的切线方程为![]() ,其中
,其中![]() 、
、![]() 、
、![]() 为常数.
为常数.
(1)函数![]() 是否存在单调递减区间?若存在,则求出单调递减区间(用
是否存在单调递减区间?若存在,则求出单调递减区间(用![]() 表示);
表示);
(2)若![]() 不是函数
不是函数![]() 的极值点,求证:函数
的极值点,求证:函数![]() 的图像关于点
的图像关于点![]() 对称.
对称.
解:(Ⅰ)![]() ,
,![]() ,
,
由题意,知![]() ,
,![]()
![]() ,
,
即![]()
![]()
1. 当![]() 时,
时,![]() ,函数
,函数![]() 在区间
在区间![]() 上单调增加,
上单调增加,
不存在单调减区间;
当![]() 时,
时,![]() ,有
,有
|
|
|
|
|
|
| + | - | + |
|
|
|
|
|
![]() 当
当![]() 时,函数
时,函数![]() 存在单调减区间,为
存在单调减区间,为![]()
2. 当![]() 时,
时, ![]() ,有
,有
|
|
|
|
|
|
| + | - | + |
|
|
|
|
|
![]() 当
当![]() 时,函数
时,函数![]() 存在单调减区间,为
存在单调减区间,为![]()
(Ⅱ)由(Ⅰ)知:若![]() 不是函数
不是函数![]() 的极值点,则
的极值点,则![]() ,
,
![]()
![]()
设点![]() 是函数
是函数![]() 的图像上任意一点,则
的图像上任意一点,则![]() ,
,
点![]() 关于点
关于点![]() 的对称点为
的对称点为![]() ,
,
![]()
(或  )
)
![]() 点
点![]() 在函数
在函数![]() 的图像上.
的图像上.
由点![]() 的任意性知函数
的任意性知函数![]() 的图像关于点
的图像关于点![]() 对称.
对称.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
 ,在函数
,在函数 图像上一点
图像上一点 处切线的斜率为3.
处切线的斜率为3. 在
在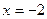 时有极值,求
时有极值,求 )若函数
)若函数 上单调递增,求
上单调递增,求 的取值范围.
的取值范围.