题目内容
(文科做)已知数列{an}满足递推式:an-an-1=2n-1,(n≥2,n∈N)且a1=1.
(1)求a2,a3;
(2)求an;
(3)若bn=(-1)nan,求数列{bn}的前n项之和Tn.
解:(1)∵a2-a1=2×1+1=3,
∴a2=4,
又a3-a1=2×2+1=5,
∴a3=9.
(2)由an-an-1=2n-1,
知an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=1+3+5+…+(2n-1)=n2.
(3)∵
= .
.
记 ,
,
则bn=f(n)-f(n-1)(n≥2),
又b1=f(1),
∴Tn=(f(n)-f(n-1))+…+(f(2)-f(1))+f(1)
=
= ,
,
∴ .
.
分析:(1)由a2-a1=2×1+1=3,知a2=4,再由a3-a1=2×2+1=5,能求出a3.
(2)由an-an-1=2n-1,用累加法能求出an.
(3)由 =
= ,记
,记 ,则bn=f(n)-f(n-1)(n≥2),再由b1=f(1),能求出Tn.
,则bn=f(n)-f(n-1)(n≥2),再由b1=f(1),能求出Tn.
点评:本题考查数列知识的综合运用,解题时要认真审题,仔细解答,注意数列递推式的灵活运用.
∴a2=4,
又a3-a1=2×2+1=5,
∴a3=9.
(2)由an-an-1=2n-1,
知an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=1+3+5+…+(2n-1)=n2.
(3)∵

=
 .
.记
 ,
,则bn=f(n)-f(n-1)(n≥2),
又b1=f(1),
∴Tn=(f(n)-f(n-1))+…+(f(2)-f(1))+f(1)
=

=
 ,
,∴
 .
.分析:(1)由a2-a1=2×1+1=3,知a2=4,再由a3-a1=2×2+1=5,能求出a3.
(2)由an-an-1=2n-1,用累加法能求出an.
(3)由
 =
= ,记
,记 ,则bn=f(n)-f(n-1)(n≥2),再由b1=f(1),能求出Tn.
,则bn=f(n)-f(n-1)(n≥2),再由b1=f(1),能求出Tn.点评:本题考查数列知识的综合运用,解题时要认真审题,仔细解答,注意数列递推式的灵活运用.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
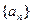 满足递推式
满足递推式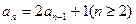 ,其中
,其中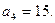
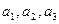 ;
; 并求数列
并求数列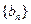 有
有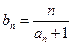 求数列
求数列 的前n项和
的前n项和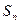 .
. 满足递推式
满足递推式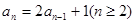 ,其中
,其中
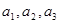 ;
; 并求数列
并求数列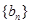 有
有 求数列
求数列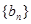 的前n项和
的前n项和 .
.