题目内容
已知函数f（x）=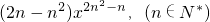
在（0，+∞）是增函数．
（1）求f（x）的解析式；
（2）设g（x）=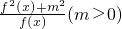
，试判断g（x）在（0，+∞）上的单调性，并加以证明．
解：由题意（1）
；
∵n∈N*∴n=1?f（x）=x；
（2）
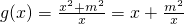
设0＜x1＜x2，则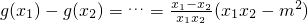
；
若0＜x1＜x2≤m，则x1x2＜m2；若m≤x1＜x2，则x1x2＞m2；而x1x2＞0，x1-x2＜0
当0＜x1＜x2≤m时，g（x1）＞g（x2）；当m≤x1＜x2时，g（x1）＜g（x2）
因此，g（x）在（0，m]上单调递减；g（x）在[m，+∞）上单调递增；
分析：（1）利用函数在（0，+∞）是增函数，可建立不等式组，从而可求n的值，进而可求f（x）的解析式；
（2）先表达出g（x），再利用定义判断并证明函数在（0，+∞）上的单调性
点评：本题以具体函数为载体，考查函数的性质，关键是正确理解与运用单调性的定义．
；∵n∈N*∴n=1?f（x）=x；
（2）
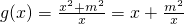
设0＜x1＜x2，则
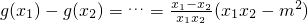；若0＜x1＜x2≤m，则x1x2＜m2；若m≤x1＜x2，则x1x2＞m2；而x1x2＞0，x1-x2＜0
当0＜x1＜x2≤m时，g（x1）＞g（x2）；当m≤x1＜x2时，g（x1）＜g（x2）
因此，g（x）在（0，m]上单调递减；g（x）在[m，+∞）上单调递增；
分析：（1）利用函数在（0，+∞）是增函数，可建立不等式组，从而可求n的值，进而可求f（x）的解析式；
（2）先表达出g（x），再利用定义判断并证明函数在（0，+∞）上的单调性
点评：本题以具体函数为载体，考查函数的性质，关键是正确理解与运用单调性的定义．
练习册系列答案
相关题目