题目内容
已知点A(3,3),B(5,2)到直线l的距离相等,且直线l经过两直线l1:3x-y-1=0和l2:x+y-3=0的交点,求直线l的方程.
x+2y-5=0或x-6y+11=0
解:解方程组 得交点P(1,2).
得交点P(1,2).
①若点A,B在直线l的同侧,则l∥AB.
而kAB= =-
=- ,
,
由点斜式得直线l的方程为y-2=- (x-1),
(x-1),
即x+2y-5=0.
②若点A,B在直线l的异侧,则直线l经过线段AB的中点(4, ),
),
由两点式得直线l的方程为 =
= ,
,
即x-6y+11=0.
综上所述,直线l的方程为x+2y-5=0或x-6y+11=0.
 得交点P(1,2).
得交点P(1,2).①若点A,B在直线l的同侧,则l∥AB.
而kAB=
 =-
=- ,
,由点斜式得直线l的方程为y-2=-
 (x-1),
(x-1),即x+2y-5=0.
②若点A,B在直线l的异侧,则直线l经过线段AB的中点(4,
 ),
),由两点式得直线l的方程为
 =
= ,
,即x-6y+11=0.
综上所述,直线l的方程为x+2y-5=0或x-6y+11=0.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 两点,且在
两点,且在 轴上截得的线段长为
轴上截得的线段长为 ,半径小于5.(1)求直线
,半径小于5.(1)求直线 与圆C的方程;(2)若直线
与圆C的方程;(2)若直线 ,直线
,直线 与圆C交于点A、B,且以AB为直径的圆经过坐标原点,求直线
与圆C交于点A、B,且以AB为直径的圆经过坐标原点,求直线 到定点
到定点 的距离比到直线
的距离比到直线 的距离小1.
的距离小1. 的方程;
的方程; ,任作弦
,任作弦 ,满足
,满足 ,则弦
,则弦 是否经过一个定点?若经过定点(设为点
是否经过一个定点?若经过定点(设为点 ),请写出
),请写出



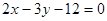 与坐标轴围成的三角形的面积为 .
与坐标轴围成的三角形的面积为 .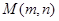 为圆C上任意一点,求
为圆C上任意一点,求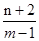 的最大值与最小值;
的最大值与最小值; 和
和 互相平行,则
互相平行,则 等于( )
等于( )