题目内容
 如图,点O是半径为l的球心,点A、B、C在此球面上,OA、OB、OC两两垂直,E、F分别是大圆弧
如图,点O是半径为l的球心,点A、B、C在此球面上,OA、OB、OC两两垂直,E、F分别是大圆弧 与
与 的中点,
的中点,
(1)求异面直线OE与AC的夹角的大小;
(2)求点E、F在该球面上的球面距离.
解: (1)连AB、BC、AC,分别取AB、BC、AC的中点D、H、M,
(1)连AB、BC、AC,分别取AB、BC、AC的中点D、H、M,
则 ,
, ,而OE∥AC
,而OE∥AC
所以∠ODH就是异面直线OE与AC所成的角或其邻补角,等于 (2分)
(2分)
所以异面直线OE与AC的夹角的大小为 (3分)
(3分)
(2)如图,作EG⊥OA于点G,连EG、EF、FG,

∴ (5分)
(5分)
∴ ,
,
∴E、F,在该球面上的球面距离为 (7分)
(7分)
分析:(1)连AB、BC、AC,分别取AB、BC、AC的中点D、H、M,欲求异面直线OE与AC的夹角的大小,而OE∥AC,得出∠ODH就是异面直线OE与AC所成的角或其邻补角,利用等边三角即可求出此角的大小;
(2)过E、F做AO的垂面交AO于G,求出EG,EF,然后求出∠EOF,利用扇形弧长公式求球面距离即可.
点评:本小题主要考查异面直线及其所成的角、球面距离及相关计算等基础知识,考查运算求解能力,考查空间想象力.属于基础题.
 (1)连AB、BC、AC,分别取AB、BC、AC的中点D、H、M,
(1)连AB、BC、AC,分别取AB、BC、AC的中点D、H、M,则
 ,
, ,而OE∥AC
,而OE∥AC所以∠ODH就是异面直线OE与AC所成的角或其邻补角,等于
 (2分)
(2分)所以异面直线OE与AC的夹角的大小为
 (3分)
(3分)(2)如图,作EG⊥OA于点G,连EG、EF、FG,

∴
 (5分)
(5分)∴
 ,
,∴E、F,在该球面上的球面距离为
 (7分)
(7分)分析:(1)连AB、BC、AC,分别取AB、BC、AC的中点D、H、M,欲求异面直线OE与AC的夹角的大小,而OE∥AC,得出∠ODH就是异面直线OE与AC所成的角或其邻补角,利用等边三角即可求出此角的大小;
(2)过E、F做AO的垂面交AO于G,求出EG,EF,然后求出∠EOF,利用扇形弧长公式求球面距离即可.
点评:本小题主要考查异面直线及其所成的角、球面距离及相关计算等基础知识,考查运算求解能力,考查空间想象力.属于基础题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 12、如图,圆O的半径为定长r,A是圆O外一定点,P是圆上任意一点.线段AP的垂直平分线l 和直线OP相交于点Q,当点P在圆上运动时,点Q的轨迹是( )
12、如图,圆O的半径为定长r,A是圆O外一定点,P是圆上任意一点.线段AP的垂直平分线l 和直线OP相交于点Q,当点P在圆上运动时,点Q的轨迹是( )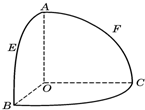 如图,O是半径为l的球心,点A、B、C在球面上,OA、OB、OC两两垂直,E、F分别是大圆弧AB与AC的中点,则点E、F在该球面上的球面距离是( )
如图,O是半径为l的球心,点A、B、C在球面上,OA、OB、OC两两垂直,E、F分别是大圆弧AB与AC的中点,则点E、F在该球面上的球面距离是( )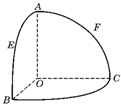 如图,点O是半径为l的球心,点A、B、C在此球面上,OA、OB、OC两两垂直,E、F分别是大圆弧
如图,点O是半径为l的球心,点A、B、C在此球面上,OA、OB、OC两两垂直,E、F分别是大圆弧
 与
与 的中点,
的中点,