题目内容
已知点P是抛物线C:y=
x2上的动点,直线l:y=x-2,则点P到直线l的最短距离为( )
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:利用点到直线的距离公式,结合配方法,即可得到结论.
解答:解:设抛物线y=
x2上的点的坐标为(x,y),则
由点到直线的距离公式可得d=
=
=
≥
.
故选:C.
| 1 |
| 2 |
由点到直线的距离公式可得d=
| |x-y-2| | ||
|
|x-
| ||
|
|-
| ||||
|
3
| ||
| 4 |
故选:C.
点评:本题考查点到直线的距离公式,考查配方法的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 已知抛物线的顶点在坐标原点O,焦点F在x轴正半轴上,倾斜角为锐角的直线l过F点,设直线l与抛物线交于A、B两点,与抛物线的准线交于M点,
已知抛物线的顶点在坐标原点O,焦点F在x轴正半轴上,倾斜角为锐角的直线l过F点,设直线l与抛物线交于A、B两点,与抛物线的准线交于M点,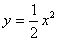 上一动点, 直线l 过点P且与抛物线C在点P处的切线垂直, l与抛物线C相交于另一点Q, 则线段PQ的中点M到x轴的最短距离是(
)
上一动点, 直线l 过点P且与抛物线C在点P处的切线垂直, l与抛物线C相交于另一点Q, 则线段PQ的中点M到x轴的最短距离是(
)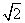 B.
B.