题目内容
ABCD是矩形,AB=a,BC=b(a>b),沿对角线AC把△ADC折起,使AD⊥BC.(1)求证:BD是异面直线AD与BC的公垂线;
(2)求BD的长.
分析:(1)由于ABCD是矩形,则AB⊥BC,因为AD⊥BC,故BC⊥平面ABD,即BC⊥BD;又AD⊥DC,AD⊥BC,即AD⊥平面BCD,即BD⊥AD,即可得证.
(2)由(1)得,在直角三角形ABD中,AB=a,BC=b(a>b),得BD=
.
(2)由(1)得,在直角三角形ABD中,AB=a,BC=b(a>b),得BD=
| a2-b2 |
解答:解:(1)由于ABCD是矩形,则AB⊥BC,
因为AD⊥BC,故BC⊥平面ABD,即BC⊥BD;
又AD⊥DC,AD⊥BC,即AD⊥平面BCD,
即BD⊥AD,
又易知AD与BC是异面直线.
故可得BD是异面直线AD与BC的公垂线.
(2)由(1)得,在直角三角形ABD中,
AB=a,BC=b(a>b),
故得BD=
.
因为AD⊥BC,故BC⊥平面ABD,即BC⊥BD;
又AD⊥DC,AD⊥BC,即AD⊥平面BCD,
即BD⊥AD,
又易知AD与BC是异面直线.
故可得BD是异面直线AD与BC的公垂线.
(2)由(1)得,在直角三角形ABD中,
AB=a,BC=b(a>b),
故得BD=
| a2-b2 |
点评:此题主要考查异面直线的角度及余弦值计算.

练习册系列答案
相关题目
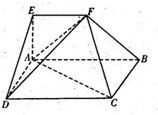 如图,在多面体ABCDEF中,四边形ABCD是矩形,AB∥EF,∠EAB=90°,AB=2,AD=AE=EF=1,平面ABFE⊥平面ABCD.
如图,在多面体ABCDEF中,四边形ABCD是矩形,AB∥EF,∠EAB=90°,AB=2,AD=AE=EF=1,平面ABFE⊥平面ABCD.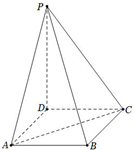 如图,已知:ABCD是矩形,AB=1,BC=2,PD⊥平面ABCD,且PD=3.
如图,已知:ABCD是矩形,AB=1,BC=2,PD⊥平面ABCD,且PD=3. (2013•深圳二模)如图,已知四边形 ABCD 是矩形,AB=2BC=2,三角形 PAB 是正三角形,且 平面 ABCD⊥平面 PCD.
(2013•深圳二模)如图,已知四边形 ABCD 是矩形,AB=2BC=2,三角形 PAB 是正三角形,且 平面 ABCD⊥平面 PCD. (2010•吉安二模)如图所示的几何体中,底面ABCD是矩形,AB=9,BC=6,EF∥平面ABCD,EF=3,△ADE和△BCF
(2010•吉安二模)如图所示的几何体中,底面ABCD是矩形,AB=9,BC=6,EF∥平面ABCD,EF=3,△ADE和△BCF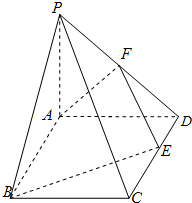 如图已知四棱锥P-ABCD中,PA⊥面ABCD,底面ABCD是矩形,
如图已知四棱锥P-ABCD中,PA⊥面ABCD,底面ABCD是矩形,