Question

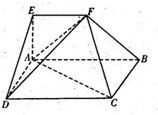如图，在多面体ABCDEF中，四边形ABCD是矩形，AB∥EF，∠EAB=90°，AB=2，AD=AE=EF=1，平面ABFE⊥平面ABCD．
（1）若点O为线段AC的中点，求证：OF∥平面ADE；
（2）求四面体ACEF的体积．

Answer 1

分析：（1）要证明OF∥平面ADE，关键要在平面ADE中找到一条可能与OF平行的直线，则△EAD边AD上的中线可能符合要求，添加辅助线后，利用平行四边形的性质，即可得到结论．
（2）根据面面平行的性质定理，BC即为平面ABFE上的高，求出△AEF的面积，并将其代入棱锥体积公式，即可得到答案．

解答：证明：（1）∵平面ABFE⊥平面ABCD，∠EAB=90°，即EA⊥AB
∴EA⊥平面ABCD．
作EH∥EA交AB于H，
∵AB=2，AD=AE=EF=1，
∴H为AB的中点
连接OH，则OH为三角形ABC的中位线，
∴OH∥BC∥AD
又由OH∩FH=H
∴平面FHO∥平面EAD，OH?平面FHO
∴OF∥平面ADE；
解：（2）S_△AEF=

1

2

•AE•EF=

1

2

∵平面ABEF⊥平面ABCD
即BC⊥AB
而平面ABEF∩平面ABCD=AB
∴BC⊥平面ABFE
∴V_C-AEF=

1

3

•S_△AEF•BC=

1

6

点评：本题考查的知识点是棱锥的体积公式，直线 与平面平行的判定，证明线面平行，找到面内与已知直线平等的直线是关键，求三棱锥的体积，确定底面和高是关键．