Question

若点A（m，0）到双曲线

x2

4

-y2=1的实轴的一个端点的距离是A到双曲线上的各个点的距离的最小值，则m的取值范围是（　　）

• A、[-2，2]
• B、[-

  5

  ，

  5

  ]
• C、[-

  5

  2

  ，

  5

  2

  ]
• D、(-∞，-

  3

  2

  ]∪[

  3

  2

  ，+∞)

Answer 1

分析：依题意，当-2≤m＜0时，点A（m，0）到双曲线的左顶点的距离最短，当0＜m≤2时，点A（m，0）到双曲线的右顶点的距离最短，再分m＞2与m＜-2讨论即可求得答案．

解答：解：由题意知双曲线

x2

4

-y²=1焦点在x轴上，且a=2，b=1，c=

5

，
∴双曲线的左、右顶点分别为为M（-2，0）、N（2，0）；

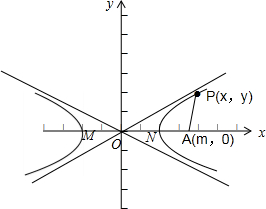
显然，当-2≤m＜0时，点A（m，0）到双曲线的左顶点的距离最短，
当0＜m≤2时，点A（m，0）到双曲线的右顶点的距离最短，
当m=0时，点A（m，0）到双曲线的左、右顶点的距离相等且最短；
当m＞2时，设双曲线右支上任意一点P（x，y），
|PA|²=（x-m）²+y²=（x-m）²+

x2

4

-1≥|AN|²=（2-m）²，
∴x²-2mx+

x2

4

-1≥4-4m，
∴（2x-4）m≤

5

4

x²-5=

5

4

（x²-4），
∵x≥2，
∴m≤

5

8

（x+2），又（x+2）_min=4，
∴m≤

5

2

，
综上，2＜m≤

5

2

时，点A（m，0）到双曲线的右顶点的距离最短；
同理可得，当-

5

2

≤m＜-2时，点A（m，0）到双曲线的左顶点的距离最短．
综上所述，当-

5

2

≤m≤

5

2

时，满足题意．
故选：C．

点评：本题考查双曲线的简单性质，着重考查两点间的距离公式，突出分类讨论思想的考查，属于难题．