题目内容
4．为了解城市居民的健康状况，某调查机构从一社区的120名年轻人，80名中年人，60名老年人中，用分层抽样方法抽取了一个容量为n的样本进行调查，其中老年人抽取了3名，则n=（ ）| A． | 26 | B． | 24 | C． | 20 | D． | 13 |
分析 根据分层抽样的应用，根据条件建立比例关系是解决本题的关键．比较基础．
解答 解：由分层抽样得$\frac{n}{120+80+60}$=$\frac{3}{60}$，
解得n=13，
故选：D．
点评 本题主要考查分层抽样的应用，根据条件建立比例关系是解决本题的关键．比较基础．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
14．经统计，2015年，某公路在部分界桩附近发生的交通事故次数如下表：
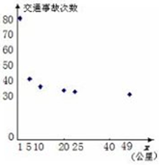
（Ⅰ）把界桩公里数1001记为x=1，公里数1005记为x=5，…，数据绘成的散点图如图所示，以x为解释变量、交通事故数y为预报变量，请在y=a+be-x和y=a+$\frac{b}{x}$间选取一个建立回归方程表述x，y二者之间的关系（a，b的值精确到0.1）；
（Ⅱ）若保险公司在2015年交通事故中随机抽取100例，理赔60万元的有1例，理赔2万元的有19例，理赔0.2万元的有80例．
利用你得到的回归方程，试预报这一年在界桩1040公里附近处发生的交通事故的理赔费（理赔费精确到0.1万元）．
附：回归直线v=$\widehat{α}$+$\widehat{β}$u的斜率和截距的最小二乘法估计分别为：
$\widehat{β}$=$\frac{\sum_{i=1}^{n}（{u}_{i}-\overline{u}）（{v}_{i}-\overline{v}）}{\sum_{i=1}^{n}（{u}_{i}-\overline{u}）^{2}}$，$\widehat{α}$=$\overline{v}$-$\widehat{β}$$\overline{u}$．
一些量的计算值：
表中：ωi=$\frac{1}{{x}_{i}}$，$\overline{ω}$=$\frac{1}{6}$$\sum_{i=1}^{6}{ω}_{i}$；φi=e${\;}^{-{x}_{i}}$，$\overline{φ}$=$\frac{1}{6}$$\sum_{i=1}^{6}{φ}_{i}$，$\frac{1}{40}$=0.025，e-40≈0．
| 界桩公里数 1001 | 1005 | 1010 | 1020 | 1025 | 1049 |
| 交通事故数 80 | 40 | 35 | 33 | 32 | 30 |
（Ⅰ）把界桩公里数1001记为x=1，公里数1005记为x=5，…，数据绘成的散点图如图所示，以x为解释变量、交通事故数y为预报变量，请在y=a+be-x和y=a+$\frac{b}{x}$间选取一个建立回归方程表述x，y二者之间的关系（a，b的值精确到0.1）；
（Ⅱ）若保险公司在2015年交通事故中随机抽取100例，理赔60万元的有1例，理赔2万元的有19例，理赔0.2万元的有80例．
利用你得到的回归方程，试预报这一年在界桩1040公里附近处发生的交通事故的理赔费（理赔费精确到0.1万元）．
附：回归直线v=$\widehat{α}$+$\widehat{β}$u的斜率和截距的最小二乘法估计分别为：
$\widehat{β}$=$\frac{\sum_{i=1}^{n}（{u}_{i}-\overline{u}）（{v}_{i}-\overline{v}）}{\sum_{i=1}^{n}（{u}_{i}-\overline{u}）^{2}}$，$\widehat{α}$=$\overline{v}$-$\widehat{β}$$\overline{u}$．
一些量的计算值：
| $\overline{x}$ | $\overline{y}$ $\overline{ω}$ $\overline{φ}$ | $\sum_{i=1}^{6}（{ω}_{i}-\overline{ω}）^{2}$ | $\sum_{i=1}^{6}（{φ}_{i}-\overline{φ}）^{2}$ | $\sum_{i=1}^{6}（{ω}_{i}-\overline{ω}）（{y}_{i}-\overline{y}）$ | $\sum_{i=1}^{6}（{φ}_{i}-\overline{φ}）（{y}_{i}-\overline{y}）$ |
| 18.3 | 41.7 0.235 0.062 | 0.723 | 0.112 | 36.3 | 14.1 |
19．在△ABC中，a，b，c分别为角A，B，C所对的边，若b=$\sqrt{2}$，a=2，B=$\frac{π}{4}$，则c=（ ）
| A． | $\frac{1}{2}$ | B． | $\sqrt{2}$ | C． | 2 | D． | $\sqrt{3}$ |
16．
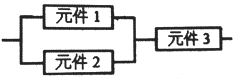某个部件由三个元件按图方式连接而成，元件1或元件2正常工作，且元件3正常工作，则部件正常工作（其中元件1，2，3正常工作的概率都为$\frac{1}{2}$），设三个电子元件的使用寿命（单位：小时）均服从正态分布N（1000，502），且各个元件能否正常工作相互独立，那么该部件的使用寿命超过1000小时的概率为（ ）
某个部件由三个元件按图方式连接而成，元件1或元件2正常工作，且元件3正常工作，则部件正常工作（其中元件1，2，3正常工作的概率都为$\frac{1}{2}$），设三个电子元件的使用寿命（单位：小时）均服从正态分布N（1000，502），且各个元件能否正常工作相互独立，那么该部件的使用寿命超过1000小时的概率为（ ）| A． | $\frac{3}{4}$ | B． | $\frac{1}{4}$ | C． | $\frac{5}{8}$ | D． | $\frac{3}{8}$ |
13．在等差数列{an}中，a7a11=6，a4+a14=5，则该数列公差d等于（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$或$-\frac{1}{2}$ | C． | -$\frac{1}{4}$ | D． | $\frac{1}{4}$或-$\frac{1}{4}$ |
14．若实数a，b，c满足对任意实数x，y有3x+4y-5≤ax+by+c≤3x+4y+5，则（ ）
| A． | a+b-c的最小值为2 | B． | a-b+c的最小值为-4 | ||
| C． | a+b-c的最大值为4 | D． | a-b+c的最大值为6 |