题目内容
已知向量 =(
=( cosx+
cosx+ sinx,cosx),
sinx,cosx), =(cosx-sinx,2sinx),f(x)=
=(cosx-sinx,2sinx),f(x)= •
• .
.(Ⅰ)求f(x)的最小正周期及单调增区间;
(Ⅱ)a,b,c分别△ABC的三内角A,B,C的对应边,且f(A)=
 ,b=2c,a=2
,b=2c,a=2 ,求S△ABC.
,求S△ABC.
【答案】分析:(1)利用两角和差的正弦公式化简f(x)的解析式为2sin(2A+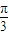 ),由此求得最小正周期.由
),由此求得最小正周期.由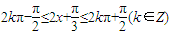 ,求得f(x)单调区间.
,求得f(x)单调区间.
(2)由f(A)=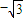 解得sin(2A+
解得sin(2A+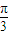 )=-
)=-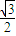 .再由A的范围可得2A+
.再由A的范围可得2A+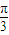 =
= 或2A+
或2A+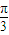 =
=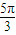 ,从而求出A的值,
,从而求出A的值,
再由余弦定理求出c的值,代入S△ABC= bc•sinA运算求得结果.
bc•sinA运算求得结果.
解答:解:(1)f(x)=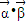 =(
=(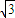 cosx+
cosx+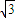 sinx)(cosx-sinx)+cosx2sinx
sinx)(cosx-sinx)+cosx2sinx
=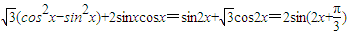 ,
,
故最小正周期T=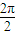 =π.
=π.
令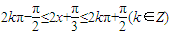 ,解得
,解得 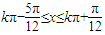 ,k∈Z.
,k∈Z.
故f(x)单调区间为[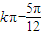 ,
,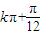 ](k∈Z).
](k∈Z).
(2)由f(A)=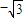 ,可得 2sin(2A+
,可得 2sin(2A+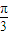 )=-
)=-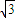 ,sin(2A+
,sin(2A+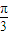 )=-
)=-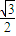 .
.
由于 0<A<π,∴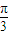 <2A+
<2A+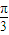 <
< ,∴2A+
,∴2A+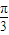 =
=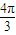 或2A+
或2A+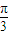 =
=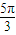 .
.
解得 A=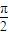 或A=
或A=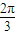 .
.
当 A= 时,由勾股定理可得 20=b2+c2=5c2,∴c=2,故S△ABC=
时,由勾股定理可得 20=b2+c2=5c2,∴c=2,故S△ABC=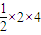 =4.
=4.
当 A=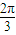 时,由余弦定理可得 20=b2+c2-2bc•cos
时,由余弦定理可得 20=b2+c2-2bc•cos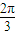 =7c2,
=7c2,
故 S△ABC= bc•sin
bc•sin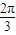 =
=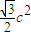 =
=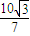 .
.
点评:本题主要考查两角和差的正弦公式,正弦函数的周期性和单调性,余弦定理的应用,体现了分类讨论的数学思想,属于中档题.
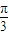 ),由此求得最小正周期.由
),由此求得最小正周期.由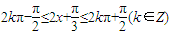 ,求得f(x)单调区间.
,求得f(x)单调区间.(2)由f(A)=
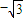 解得sin(2A+
解得sin(2A+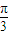 )=-
)=-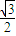 .再由A的范围可得2A+
.再由A的范围可得2A+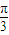 =
= 或2A+
或2A+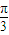 =
=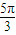 ,从而求出A的值,
,从而求出A的值,再由余弦定理求出c的值,代入S△ABC=
 bc•sinA运算求得结果.
bc•sinA运算求得结果.解答:解:(1)f(x)=
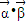 =(
=(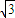 cosx+
cosx+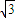 sinx)(cosx-sinx)+cosx2sinx
sinx)(cosx-sinx)+cosx2sinx =
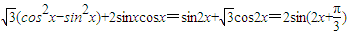 ,
,故最小正周期T=
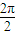 =π.
=π.令
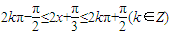 ,解得
,解得 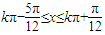 ,k∈Z.
,k∈Z.故f(x)单调区间为[
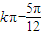 ,
,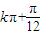 ](k∈Z).
](k∈Z).(2)由f(A)=
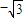 ,可得 2sin(2A+
,可得 2sin(2A+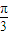 )=-
)=-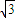 ,sin(2A+
,sin(2A+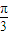 )=-
)=-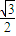 .
.由于 0<A<π,∴
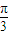 <2A+
<2A+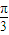 <
< ,∴2A+
,∴2A+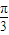 =
=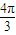 或2A+
或2A+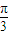 =
=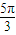 .
.解得 A=
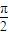 或A=
或A=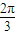 .
.当 A=
 时,由勾股定理可得 20=b2+c2=5c2,∴c=2,故S△ABC=
时,由勾股定理可得 20=b2+c2=5c2,∴c=2,故S△ABC=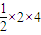 =4.
=4.当 A=
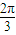 时,由余弦定理可得 20=b2+c2-2bc•cos
时,由余弦定理可得 20=b2+c2-2bc•cos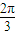 =7c2,
=7c2,故 S△ABC=
 bc•sin
bc•sin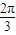 =
=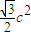 =
=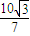 .
.点评:本题主要考查两角和差的正弦公式,正弦函数的周期性和单调性,余弦定理的应用,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目