题目内容
6.将函数y=sin(x+$\frac{π}{6}$)(x∈R)的图象上所有的点向左平移$\frac{π}{4}$个单位长度,所得图象的函数解析式为( )| A. | y=sin(x+$\frac{π}{12}$) | B. | y=sin(x-$\frac{π}{12}$) | C. | y=sin(x+$\frac{5π}{12}$) | D. | y=sin(x-$\frac{5π}{12}$) |
分析 根据y=Asin(ωx+φ)的图象变换规律可得结论.
解答 解:把函数y=sin(x+$\frac{π}{6}$)的图象向左平移$\frac{π}{4}$个单位所得图象的函数解析式为:
y=sin[(x+$\frac{π}{4}$)+$\frac{π}{6}$]=sin(x+$\frac{5π}{12}$).
故选:C.
点评 本题主要考查y=Asin(ωx+φ)的图象变换规律,属于中档题.

练习册系列答案
相关题目
16.已知锐角三角形三边长分别为1,3,a,则a的取值范围是( )
| A. | 8<a<10 | B. | 2$\sqrt{2}<a<\sqrt{10}$ | C. | $2\sqrt{2}<a<10$ | D. | $\sqrt{10}<a<8$ |
1.已知双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的焦距为10,一条渐近线为y=$\frac{1}{2}$x,则该双曲线的方程为( )
| A. | $\frac{{x}^{2}}{20}-\frac{{y}^{2}}{5}$=1 | B. | $\frac{{x}^{2}}{5}-\frac{{y}^{2}}{20}$=1 | C. | $\frac{{x}^{2}}{80}-\frac{{y}^{2}}{20}$=1 | D. | $\frac{{x}^{2}}{20}-\frac{{y}^{2}}{80}$=1 |
11.若a=log20.5,b=20.5,c=0.52,则a,b,c三个数的大小关系是( )
| A. | a<b<c | B. | b<c<a | C. | a<c<b | D. | c<a<b |
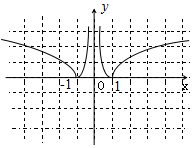 已知函数f(x)是定义在{x|x≠0}上的偶函数,且当x>0时,f(x)=log2x.
已知函数f(x)是定义在{x|x≠0}上的偶函数,且当x>0时,f(x)=log2x.