题目内容
(本小题满分12分)
设数列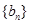 的前
的前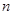 项和为
项和为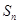 ,且
,且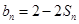 ;数列
;数列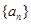 为等差数列,且
为等差数列,且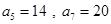 .
.
(1)求数列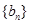 的通项公式;
的通项公式;
(2)若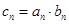 (
(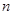 =1,2,3…),
=1,2,3…),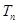 为数列
为数列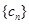 的前
的前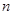 项和.求
项和.求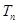 .
.
设数列
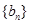 的前
的前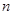 项和为
项和为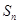 ,且
,且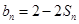 ;数列
;数列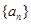 为等差数列,且
为等差数列,且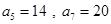 .
.(1)求数列
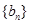 的通项公式;
的通项公式;(2)若
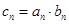 (
(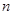 =1,2,3…),
=1,2,3…),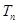 为数列
为数列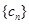 的前
的前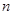 项和.求
项和.求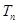 .
.(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
. (1)由已知条件bn=2-2Sn;当n=1时先求出 ,再利用
,再利用 ,
, ,得到
,得到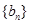 是以
是以 为首项,
为首项,  为公比的等比数列,利用等比数列的通项公式求出通项.
为公比的等比数列,利用等比数列的通项公式求出通项.
(2)求出 ,是一个等差数列与一个等比数列的乘积,所以利用错位相减的方法求出和.
,是一个等差数列与一个等比数列的乘积,所以利用错位相减的方法求出和.
(1)由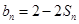 ,令
,令 ,则
,则 ,又
,又 , 所以
, 所以 ……2分
……2分
当 时,由
时,由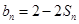 ,可得
,可得 ,即
,即 ………4分
………4分
所以 是以
是以 为首项,
为首项, 为公比的等比数列,于是
为公比的等比数列,于是 …………6分
…………6分
(2)数列 为等差数列,公差
为等差数列,公差 ,可得
,可得 …………7分
…………7分
从而
 ,
,

 ………………11分
………………11分
 . ……………………12分
. ……………………12分
 ,再利用
,再利用 ,
, ,得到
,得到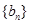 是以
是以 为首项,
为首项,  为公比的等比数列,利用等比数列的通项公式求出通项.
为公比的等比数列,利用等比数列的通项公式求出通项.(2)求出
 ,是一个等差数列与一个等比数列的乘积,所以利用错位相减的方法求出和.
,是一个等差数列与一个等比数列的乘积,所以利用错位相减的方法求出和.(1)由
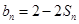 ,令
,令 ,则
,则 ,又
,又 , 所以
, 所以 ……2分
……2分当
 时,由
时,由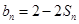 ,可得
,可得 ,即
,即 ………4分
………4分所以
 是以
是以 为首项,
为首项, 为公比的等比数列,于是
为公比的等比数列,于是 …………6分
…………6分(2)数列
 为等差数列,公差
为等差数列,公差 ,可得
,可得 …………7分
…………7分从而

 ,
,
 ………………11分
………………11分 . ……………………12分
. ……………………12分
练习册系列答案
相关题目
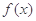 定义在区间
定义在区间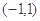 上,
上,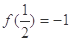 ,且当
,且当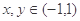 时,恒有
时,恒有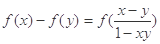 .又数列
.又数列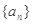 满足
满足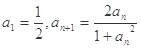 .
.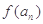 的表达式;
的表达式;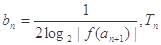 为数列
为数列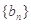 的前
的前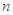 项和,若
项和,若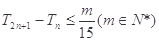 对
对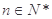 恒成立,求
恒成立,求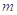 的最小值.
的最小值.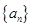 满足
满足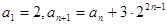 ,
,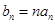 ,求数列的前n项和
,求数列的前n项和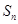 .
.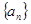 中,
中,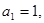 且点
且点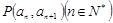 在直线
在直线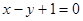 上.
上.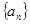 的通项公式;
的通项公式; (2)若函数
(2)若函数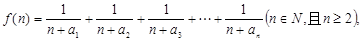 求函数
求函数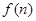 的最小值;
的最小值;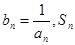 表示数列
表示数列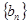 的前
的前 项和.试问:是否存在关于
项和.试问:是否存在关于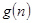 ,使得
,使得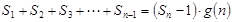 对于一切不小于2的自然数
对于一切不小于2的自然数 ,求数列{bn}的前
,求数列{bn}的前 项和Sn.
项和Sn.  中,若
中,若 ,则
,则 的值为( )
的值为( ) B
B  C
C  D
D 
 的前
的前 项和为
项和为 ,已知
,已知 ,
, 和公差
和公差 的值;
的值; ,求
,求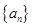 的首项为
的首项为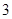 ,
,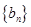 为等差数列且
为等差数列且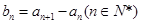 .若则
.若则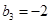 ,
,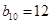 ,则
,则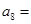 ( )
( ) 
 的公差是( )
的公差是( )