Question

已知A(4,0)、B(2,2)是椭圆内的两个点,M是椭圆上的动点.

(1)求|MA|+|MB|的最大值和最小值;

(2)求|MB|+|MA|的最小值.

Answer 1

解:

(1)如图所示,

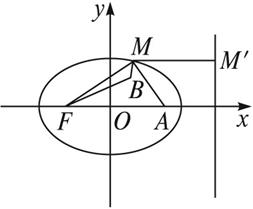
由,知a=5,b=3,c=4.

∴点A(4,0)为椭圆的右焦点,左焦点为F(-4,0).

又∵|MA|+|MF|=2a=10,

∴|MA|+|MB|=10-|MF|+|MB|.

∵||MB|-|MF||≤|BF|=,

∴-2≤|MB|-|MF|≤2.

故10-2≤|MA|+|MB|≤10+2,

即|MA|+|MB|的最大值为10+2,最小值为10-2.

(2)由题意,椭圆的右准线为x=,设M到右准线的距离为|MM′|,由椭圆第二定义,知,

∴|MA|=|MM′|.

∴|MB|+|MA|=|MB|+|MM′|.

由图易知当B、M、M′共线时,|MB|+|MM′|最小为|BM′|=

此时M坐标为(,2).