题目内容
已知A(4,0)、B(2,2)是椭圆
=1内的两定点,点M是椭圆上的动点,求|MA|+|MB|的最值.
解:∵A(4,0)是椭圆的右焦点,设A′为椭圆的左焦点,则A′(-4,0),由椭圆定义知|MA|+|MA′|=10,如图(1)所示.
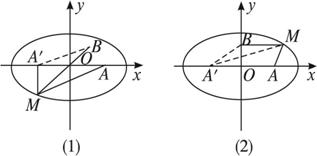
|MA|+|MB|=|MA|+|MA′|+|MB|-|MA′|=10+|MB|-|MA′|≤10+|A′B|(当点M在BA′的延长线上时取等号),
∴当M为射线BA′与椭圆的交点时,(|MA|+|MB|)max=10+|A′B|=10+2
.
又如图(2),|MA|+|MB|=|MA|+|MA′|-|MA′|+|MB|=10-(|MA′|-|MB|)≥10-|A′B|(当M在A′B的延长线上时取等号).
∴当M为射线A′B与椭圆交点时,
(|MA|+|MB|)min=10-|A′B|=10-210.
练习册系列答案
相关题目
内的两个点,M是椭圆上的动点.
|MA|的最小值.