题目内容
18．写出求函数y=2x+3图象上任意一点到原点的距离的算法，并画出相应的程序框图．分析 给出函数图象上任一点函数y=2x+3图象上任一点的横坐标x（由键盘输入），到原点的距离d=$\sqrt{{x}^{2}+{y}^{2}}$，即可画出框图，写出算法．
解答 
解：算法如下：
第一步，输入横坐标的值x．
第二步，计算y=2x+3．
第三步，计算d=$\sqrt{{x}^{2}+{y}^{2}}$．
第四步，输出d．
程序框图如下：
点评 本题主要考察设计程序框图解决实际问题，属于基础题．
练习册系列答案
相关题目
9．
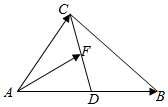如图所示，在△ABC中，AD=DB，点F在线段CD上，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AC}$=$\overrightarrow{b}$，$\overrightarrow{AF}=x$$\overrightarrow{a}$+y$\overrightarrow{b}$，则$\frac{1}{x}+\frac{4}{y+1}$的最小值为（ ）
如图所示，在△ABC中，AD=DB，点F在线段CD上，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AC}$=$\overrightarrow{b}$，$\overrightarrow{AF}=x$$\overrightarrow{a}$+y$\overrightarrow{b}$，则$\frac{1}{x}+\frac{4}{y+1}$的最小值为（ ）| A． | $6+2\sqrt{2}$ | B． | $6\sqrt{3}$ | C． | 6+4$\sqrt{2}$ | D． | $3+2\sqrt{2}$ |
3．已知点A（1，1），B（2，1），C（1，2），若λ∈[-1，2]，μ∈[2，3]，则|λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$|的取值范围是（ ）
| A． | [2，10] | B． | [$\sqrt{5}$，$\sqrt{13}$] | C． | [1，5] | D． | [2，$\sqrt{13}$] |
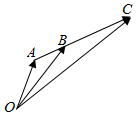已知A（2，3），B（5，4），连接AB并延长至C，使得AC=3AB，求C点的坐标．（提示：如图所示，$\overrightarrow{OC}$=$\overrightarrow{OA}$+3$\overrightarrow{AB}$）
8．若tanα=3，则tan（α-$\frac{π}{4}$）=（ ）
| A． | 2 | B． | -2 | C． | -$\frac{1}{2}$ | D． | $\frac{1}{2}$ |