题目内容
1. 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.(1)求证:AC⊥BC1,
(2)求证:AC1∥平面CDB1;
(3)求三棱锥D-AA1C1的体积.
分析 (1)由BB1⊥平面ABC得BB1⊥AC,由勾股定理的逆定理得AC⊥BC,故AC⊥平面BCC1B1,于是AC⊥BC1;'
(2)设CB1与C1B的交点为E,连接DE,由中位线定理可得DE∥AC1,于是AC1∥平面CDB1;
(3)由D为AB中点可知V${\;}_{D-A{A}_{1}{C}_{1}}$=$\frac{1}{2}$V${\;}_{B-A{A}_{1}{C}_{1}}$=$\frac{1}{2}$V${\;}_{B-AC{C}_{1}}$=$\frac{1}{2}$V${\;}_{{C}_{1}-ABC}$.
解答 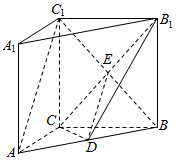 解:(1)证明:∵AC=3,AB=5,BC=4,∴AC⊥BC
解:(1)证明:∵AC=3,AB=5,BC=4,∴AC⊥BC
∵BB1⊥平面ABC,AC?平面ABC,
∴AC⊥CC1,又BC∩CC1=C,BC?平面BCC1B1,CC1?平面BCC1B1,
∴AC⊥平面BCC1B1.∵BC1?平面BCC1B1,
∴AC⊥BC1.
(2)证明:设CB1与C1B的交点为E,连接DE,
∵四边形BCC1B1是平行四边形,∴E是BC1的中点,
∵D是AB的中点,
∴DE∥AC1,又∵DE?平面CDB1,AC1?平面CDB1,
∴AC1∥平面CDB1.
(3)解:V${\;}_{B-A{A}_{1}{C}_{1}}$=V${\;}_{B-AC{C}_{1}}$=V${\;}_{{C}_{1}-ABC}$=$\frac{1}{3}{S}_{△ABC}•C{C}_{1}$=$\frac{1}{3}×\frac{1}{2}×3×4×4=8$.
∵D是AB的中点,
∴V${\;}_{D-A{A}_{1}{C}_{1}}$=$\frac{1}{2}$V${\;}_{B-A{A}_{1}{C}_{1}}$=4.
点评 本题考查了线面垂直的判定与性质,线面平行的判定,棱锥的体积计算,属于基础题.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案| A. | y=±$\sqrt{2}$x | B. | y=±2x | C. | y=±$\sqrt{3}$x | D. | y=±2$\sqrt{2}$x |
| A. | 1 | B. | 2 | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{3}$ |
 已知四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,PA⊥底面ABCD,M为AB的中点.
已知四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,PA⊥底面ABCD,M为AB的中点.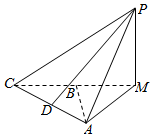 如图,在三棱锥P-AMC中,AC=AM=PM=2,PM⊥面AMC,AM⊥AC,B,D分别为CM,AC的中点.
如图,在三棱锥P-AMC中,AC=AM=PM=2,PM⊥面AMC,AM⊥AC,B,D分别为CM,AC的中点.