题目内容

若函数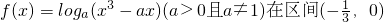 $数学公式$ 内单调递增，则实数a的取值范围是________．

$\text{[math]}$
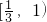
分析：将函数看作是复合函数，令g（x）=x³-ax，且g（x）＞0，得x∈（- $\text{[math]}$ ，0）∪（ $\text{[math]}$ ，+∞），因为函数是三次函数，所以用导数来判断其单调性，再由复合函数“同增异减”求得结果．
解答：令g（x）=x³-ax，则g（x）＞0．得到 x∈（- $\text{[math]}$ ，0）∪（ $\text{[math]}$ ，+∞），
由于g′（x）=3x²-a，
令g′（x）=3x²-a＞0得：x∈（-∞，- $\text{[math]}$ ）或x∈（ $\text{[math]}$ ，+∞）
故x∈（-∞，- $\text{[math]}$ ）或x∈（ $\text{[math]}$ ，+∞）时，g（x）单调递增，
x∈（- $\text{[math]}$ ， $\text{[math]}$ ）时，g（x）单调递减，?
∴当a＞1时，减区间为（- $\text{[math]}$ ，0），?不合题意，
当0＜a＜1时，（- $\text{[math]}$ ，0）为增区间．?
∴（- $\text{[math]}$ ，0）?（- $\text{[math]}$ ，0），∴- $\text{[math]}$ ≥- $\text{[math]}$ ，∴a≥ $\text{[math]}$ ．
综上，a∈[ $\text{[math]}$ ，1）．
故答案为：[ $\text{[math]}$ ，1）．
点评：本题主要考查对数函数的单调性与特殊点、复合函数的单调性、利用导数研究单调性等基础知识，解题时一定要注意定义域．属于基础题．