题目内容
已知定义域为R的函数f(x)在区间(8,+∞)上为减函数,且函数y=f(x+8)为偶函数,则
| A.f(6)>f(7) | B.f(6)>f(9) |
| C.f(7)>f(9) | D.f(7)>f(10) |
D.
解析试题分析:本题主要弄清楚函数 与
与 的图象之间的关系.函数
的图象之间的关系.函数 的图象向左平移8个单位,得到函数
的图象向左平移8个单位,得到函数 的图象,反之,函数
的图象,反之,函数 的图象可以看作是由函数
的图象可以看作是由函数 的图象向右平移8个单位得到的.函数
的图象向右平移8个单位得到的.函数 为偶函数,它的图象关于
为偶函数,它的图象关于 轴对称,因此函数
轴对称,因此函数 的图象关于直线
的图象关于直线 对称,∴
对称,∴ ,
, ,再由于函数
,再由于函数 在
在 为减函数,故正确答案为D.
为减函数,故正确答案为D.
考点:函数的图象及其对称性.

练习册系列答案
相关题目
已知定义在 上的奇函数
上的奇函数 ,满足
,满足 ,且在区间
,且在区间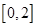 上是增函数,若方程
上是增函数,若方程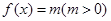 ,在区间
,在区间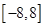 上有四个不同的根
上有四个不同的根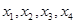 ,则
,则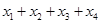 =( )
=( )
| A.-12 | B.-8 | C.-4 | D.4 |
若 为偶函数,且当
为偶函数,且当 时,
时, ,则
,则 的零点个数为 ( )
的零点个数为 ( )
A. | B. | C. | D.无穷多个 |
设函数 ,则D(x) ( )
,则D(x) ( )
| A.是偶函数而不是奇函数 | B.是奇函数而不是偶函数 |
| C.既是偶函数又是奇函数 | D.既不是偶函数也不是奇函数 |
函数 的定义域为 ( )
的定义域为 ( )
A. | B. |
C. | D. ∪ ∪ |
设函数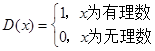 ,则下列结论错误的是( )
,则下列结论错误的是( )
| A.D(x)的值域为{0,1} | B.D(x)是偶函数 |
| C.D(x)不是周期函数 | D.D(x)不是单调函数 |
若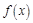 是偶函数,且当
是偶函数,且当 时,f (x) = x-1,则f (x-1) < 0的解集是( )
时,f (x) = x-1,则f (x-1) < 0的解集是( )
| A.{x |-1 < x < 0} | B.{x | x < 0或1< x < 2} |
| C.{x | 0 < x < 2} | D.{x | 1 < x < 2} |
下列函数中,既是偶函数,又在区间(1,2)内是增函数的为 ( )
A.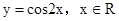 | B.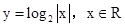 且x≠0 且x≠0 |
C.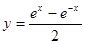 , x , x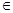 R R | D.y=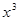 +1, x +1, x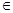 R R |
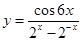 的图像大致为( )
的图像大致为( )