题目内容
(本小题满分12分)定义在R上的奇函数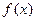 有最小正周期4,且
有最小正周期4,且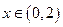 时,
时,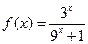 。
。
⑴求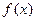 在
在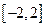 上的解析式;
上的解析式;
⑵判断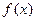 在
在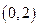 上的单调性,并给予证明;
上的单调性,并给予证明;
⑶当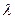 为何值时,关于方程
为何值时,关于方程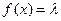 在
在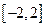 上有实数解?
上有实数解?
解:⑴当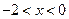 时,
时,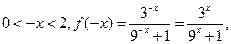
又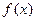 为奇函数,
为奇函数,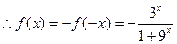 ,
,
当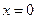 时,由
时,由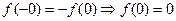
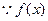 有最小正周期4,
有最小正周期4,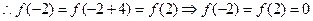 综上,
综上,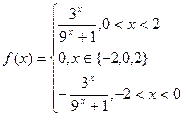
⑵设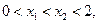 则
则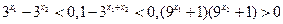
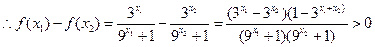
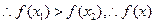 在
在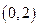 上为减函数。
上为减函数。
⑶即求函数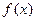 在
在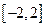 上的值域。
上的值域。
当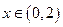 时由⑵知,
时由⑵知,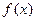 在
在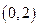 上为减函数,
上为减函数,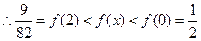 ,
,
当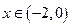 时,
时,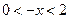 ,
,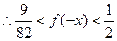 ,
,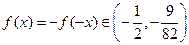
当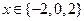 时,
时,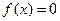
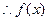 的值域为
的值域为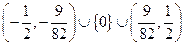
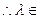
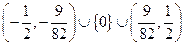 时方程方程
时方程方程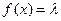 在
在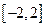
 上有实数解。
上有实数解。
解析

练习册系列答案
相关题目
函数 在
在 处的切线方程是( )
处的切线方程是( )
A.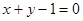 | B.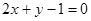 |
C. | D.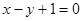 |
下列各命题中,不正确的是( )
A.若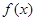 是连续的奇函数,则 是连续的奇函数,则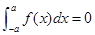 |
B.若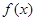 是连续的偶函数,则 是连续的偶函数,则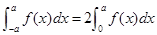 |
C.若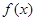 在 在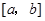 上连续且恒正,则 上连续且恒正,则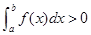 |
D.若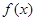 在 在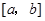 上连续,且 上连续,且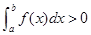 ,则 ,则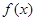 在 在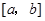 上恒正 上恒正 |
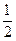 lg2+
lg2+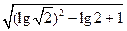 -
-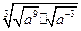 ÷
÷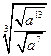 ;
;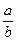 的值.
的值.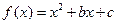 为偶函数,曲线
为偶函数,曲线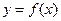 过点
过点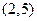 ,
,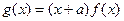 .
.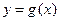 存在斜率为0的切线,求实数
存在斜率为0的切线,求实数 的取值范围;
的取值范围;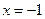 时函数
时函数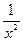 (x≠0,常数a∈R).
(x≠0,常数a∈R).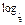 (4x-x2)的单调区间.
(4x-x2)的单调区间.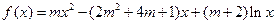 ,其中m为R上的常数,若函数
,其中m为R上的常数,若函数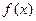 在x=1处取得极大值0,
在x=1处取得极大值0,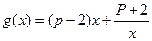 ,若对
,若对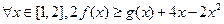 恒成立,
恒成立,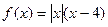 的图象并指出单调区间;
的图象并指出单调区间;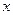 方程
方程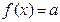 (
(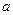 为常数)解的个数?
为常数)解的个数?